Interprétation d'une ACP sur les variables
Voici un exemple d'ACP sur les variables réalisée à partir de chiffres réels mais, pour les besoins de la présentation, avec un effectif très faible. Il reprend quelques données sur dix grands groupes américains en 2005 (source Boursorama, certains chiffres indisponibles sont estimés). Le choix des variables a été guidé par leur disponibilité. Dans la mesure où elles seront centrées et réduites par XLSTAT, il n’est pas gênant de mélanger des milliers d’euros, des effectifs et un ratio (cette diversité est voulue pour l’exemple : il n’est en effet pas très judicieux de choisir à la fois les variables « résultat net » et « RN / CP »).
Exemple
RN signifiera "résultat net", CP "capitaux propres" et CA "chiffre d'affaires".
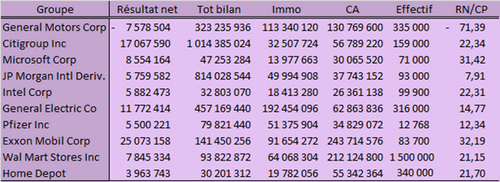
Les états de sortie suivants sont ceux de XLSTAT. Faisons l’impasse sur le tableau des statistiques descriptives et voici la matrice des corrélations de Pearson :
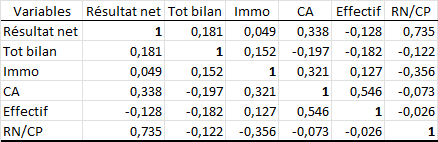
Bonne nouvelle, on ne relève pas de colinéarité (qui serait indiquée par des coefficients proches de 1). La principale corrélation est observée entre RN et RN / CP. Ceci confirme le choix malvenu de cette variable ; il aurait été plus logique de retenir « capitaux propres » que RN / CP. Même si les CP sont décorrélés du RN, ils restent en principe positifs : il existe une corrélation par le signe. Logiquement, la General Motors, seul groupe à enregistrer des pertes, contribue sensiblement à cette corrélation entre RN et RN / CP. Entrons dans le vif du sujet. Combien d’axes retenir ?
Les valeurs propres sont les suivantes :

De l’avis unanime, retenons trois axes ! Et pas seulement en respectant le critère de Kaiser : il existe bien une inflexion entre la troisième et la quatrième valeur propre, même si finalement nous n’aurons pas une belle explication de l’inertie (près de \(20\%\) restera inexpliquée). Poursuivons.
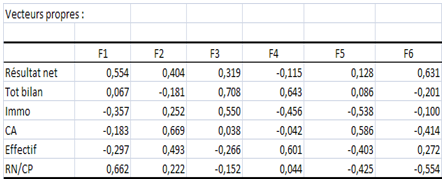
Attachons-nous aux valeurs maximales qui indiquent pour chaque axe quelle peut être sa signification. Apparemment, le premier axe isole les critères de rentabilité, le deuxième sépare davantage l’indicateur d’activité (CA) et le troisième, moins discriminant, oppose les critères de structure (postes de bilan). Le quatrième, que nous ne retenons pas, indique plutôt la taille de l'entreprise (total du bilan et effectif).
Les coordonnées des variables sur les axes factoriels confirment ces observations.
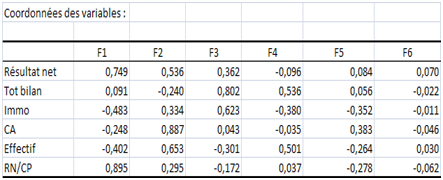
XLSTAT présente ensuite le tableau de corrélation entre variables et facteurs qui est exactement le même puisque l’ACP est normée. Ci-dessous, le tableau des contributions et les cercles des corrélations confirment nos analyses.
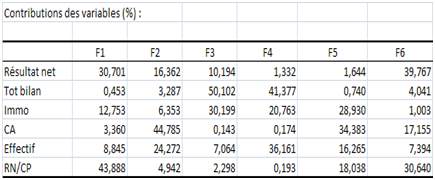
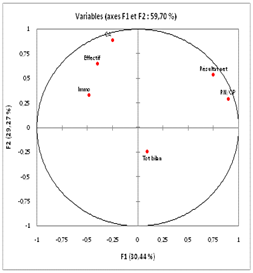
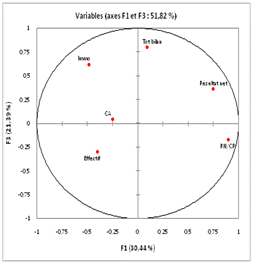
Terminons par le tableau des cosinus carrés (qualité de la représentation) :
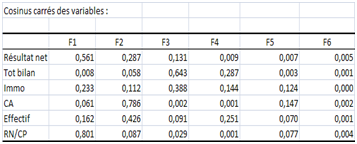
Note : le logiciel présente sur le même état de sortie l'ACP sur les individus,qui conforte l’analyse sur les variables. Attention, le faible nombre d’observations rend l’ACP sensible aux valeurs aberrantes.
Pour aller plus loin
Ce même exemple est également commenté dans le cadre de l'ACP sur individus en page résultats d'une ACP sur individus et en page contributions aux axes.
Enfin, si l’on souhaite donner une moindre importance aux outliers, on confortera l’analyse avec une ACP sur les rangs. En l’espèce, on peut même ajouter qu’il s’agit d’une bonne idée car, par leurs tailles et leurs secteurs d’activité, les dix groupes retenus présentent logiquement des valeurs très dissemblables.
