ACP et nuage des points-variables
L’analyse en composantes principales (ACP) est, n’ayons pas peur des mots, une célébrissime analyse factorielle sur variables quantitatives. Une illustration graphique constitue un peu sa « marque de fabrique ». Il s’agit du cercle des corrélations, qui se met en quatre pour vous faire découvrir des informations. Pour ceux qui n’en auraient jamais vu, en voici un bel exemplaire, issu de la page sur le résultat d’une ACP sur les variables et réalisé avec XLSTAT.
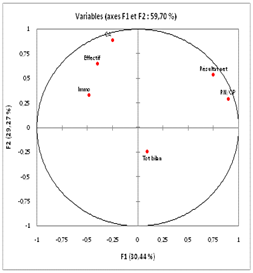
Grâce à lui, il est commode d’interpréter les composantes principales. Mais au fait, pourquoi cette figure si particulière ?
Quelques rappels
Soit une distribution bivariée. Les variables sont centrées. Le centrage consiste à retirer la moyenne de chaque valeur prise par la variable brute. Par conséquent, la variable centrée a pour moyenne 0. Cette translation est très courante en statistiques.
Généralement, les variables sont aussi réduites. La réduction consiste à diviser la variable centrée par son écart-type. Ainsi, deux variables centrées et réduites ont non seulement la même moyenne nulle, mais aussi la même dispersion égale à 1. On peut choisir de ne pas réduire les variables et l’on situe alors dans le cadre un peu particulier d’une ACP non normée (que nous ne verrons pas sur cette page).
Graphiquement, un nuage de points-variables est situé dans un espace vectoriel à \(n\) dimensions, soit autant que d’unités statistiques (que l'on supposera ici non pondérées).
La distance à l’origine
La métrique utilisée est la distance euclidienne. Pour un point \(x_i\) d’une variable donnée, c’est donc le carré de son écart par rapport à l’ORIGINE (puisqu’en l’occurrence, on mesure des distances par rapport à une moyenne nulle). L’ACP sur variables se distinguera donc de l’ACP sur les individus pour laquelle le nuage de points est centré sur son barycentre. Il suffit pour s’en convaincre de faire un détour en page effet taille.
Cette fameuse métrique euclidienne est non seulement la plus célèbre des façons de mesurer une distance mais c’est aussi celle qui est habituellement utilisée en statistiques. En effet, on note un air de famille évident avec la formule de la variance :
\[V = \frac{1}{N}\sum\limits_{i = 1}^N {({x_i} - \overline x } {)^2}\]
On voit qu’il suffit de multiplier cette formule par \(N\) pour obtenir une distance euclidienne. Comme la variance de chaque variable est égale à 1, chaque longueur de variable au carré est égale à 1. L’écart-type étant la racine carrée de 1, donc 1 également, la norme est aussi égale à 1. C’est le rayon du cercle dans lequel s’inscrivent les points-variables.
Les distances entre variables
Dès lors que l’on se situe dans un disque, ou une sphère, ou une hyper-sphère au-delà de trois dimensions, les proximités sont mesurées par des ANGLES. Voyons ceci.
Partons de la distance euclidienne entre deux variables \(j\) et \(j’.\)
\[{d^2}(j,j') = \sum\limits_{i = 1}^n {{{({x_{ij}} - {x_{ij'}})}^2}} \]
Développons cette belle identité remarquable.
\[{d^2}(j,j') = \sum\limits_{i = 1}^n {x_{ij}^2 + } \sum\limits_{i = 1}^n {x_{ij'}^2 - } 2\sum\limits_{i = 1}^n {{x_{ij}}{x_{ij'}}} \]
Les deux premiers termes sont égaux à 1 puisque ce sont des carrés de distances à l’origine. Plus intéressant est le dernier (enfin quelqu’un qui n’est pas forcément égal à 1 dans cette histoire…). On retombe cette fois sur la formule de la covariance entre deux variables centrées et réduites, c’est-à-dire à un coefficient de corrélation.
Si l’on reprend la formule ci-dessus pour lui appliquer une corrélation parfaite entre deux variables, on obtient \(1 + 1 - (2 × 1) = 0.\) Distance nulle. Au pire, le coefficient vaut -1, ce qui donne \(1 + 1 + 2 = 4.\) La distance au carré maximale est de 4, donc la distance maximale vaut 2. Graphiquement, les deux points représentatifs des variables sont à l’opposé d’un cercle de rayon 1. Tout ceci est très logique…
Idem si le coefficient est nul. Les points représentant nos deux variables sont séparés d’un quart de cercle. Les vecteurs sont orthogonaux. Leur produit scalaire est nul.
Car c’est bien là une autre façon d’appréhender les proximités dans une hyper-sphère : les produits scalaires. Il est d’ailleurs assez intuitif que la proximité entre deux vecteurs est mesurée par l’angle qu’ils forment, donc par le cosinus (pour peu que ces points soient proches du cercle).
Enfin, nous avons considéré des plans générés par des axes représentant des individus statistiquement indépendants. Le système de mesure est évidemment le même dans un plan factoriel, comme illustré ci-dessous.

Illustration
Si une variable devait être parfaitement corrélée avec l’axe \(F_1,\) sa représentation se confondrait avec lui (point rouge ci-dessous). Cette situation ne se vérifie presque jamais. Si l’inertie d’une variable est complètement absorbée par les deux premières composantes principales, le point se trouve sur le cercle mais entre les deux axes \(F_1\) et \(F_2\) (point bleu). Si la corrélation est parfaite mais qu’elle est négative, par exemple avec la première composante, il se trouve sur un autre quart du cercle (point vert). Si l’inertie de la variable n’est presque pas absorbée par les deux premiers axes mais par un troisième ou par les suivants, non représentés, son point représentatif est assez loin du cercle, du moins dans le premier plan factoriel. Ceci signifie que la corrélation est faible et que cette variable ne doit pas être prise en compte à ce niveau-ci de l’analyse (point rose).
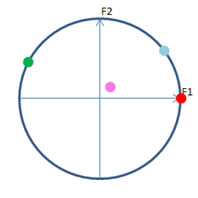
Rappel : cette opération de centrage et de réduction n’est pas réalisée sur les unités statistiques. C’est pourquoi le nuage de points-individus ne doit pas figurer dans un cercle des corrélations. Seule l’ACP sur les variables est illustrée de la sorte.
