Produit scalaire et orthogonalité
L’orthogonalité est une notion mathématique particulièrement féconde. Après une première apparition en classe de première générale dans le chapitre sur le produit scalaire, elle fait de nombreux come-back au cours des études, y compris dans le cadre de techniques statistiques élaborées. Cette notion est également enseignée dans les classes de premières STI2D et STL.
Orthogonalité et perpendicularité
Étymologiquement, orthogonal signifie angle droit. Graphiquement, lorsque deux axes gradués se croisent perpendiculairement pour former un plan, nous sommes en présence d'un repère orthogonal.
La perpendicularité est une notion très proche. Deux droites qui se croisent à angle droit (ou une droite et un plan, ou deux plans…) sont perpendiculaires. Au collège, on démontre que deux segments de droites sont perpendiculaires grâce au théorème de Pythagore. Mais l’orthogonalité est un concept plus abstrait, plus général. Ainsi, dans l’espace, deux droites peuvent se croiser « à distance », sans se toucher (comme des traînées d’avions dans le ciel vues du sol). Si ce croisement forme un angle droit, les droites ne sont pas perpendiculaires mais elles sont orthogonales.

Il en est de même de segments de droites qui seraient perpendiculaires s’ils se prolongeaient. Et donc des vecteurs dans le plan : si leurs droites supports sont perpendiculaires, alors les vecteurs sont orthogonaux. Ainsi, on n'emploie pas le terme de perpendicularité pour caractériser des vecteurs mais toujours celui d'orthogonalité.
Vecteurs orthogonaux
Deux vecteurs sont orthogonaux si leur produit scalaire est nul. C’est évident quand on se souvient de la formule du cosinus (si le cosinus de deux vecteurs est nul, c’est que ceux-ci sont orthogonaux).
Ainsi, deux droites sont perpendiculaires dans le plan si et seulement si le produit scalaire de leurs vecteurs directeurs est nul.
Le vecteur nul est considéré comme orthogonal à tous les autres vecteurs du plan.
Exemple d’application : soit un quadrilatère \(ABCD.\) Celui-ci est un losange si et seulement si le produit scalaire des vecteurs \(\overrightarrow{AC}\) et \(\overrightarrow{BD}\) est nul.
Vecteur normal
Un vecteur normal à une droite est un vecteur non nul qui est orthogonal à un vecteur directeur de cette droite.
Une droite d’équation cartésienne \(\alpha x + \beta y + \delta = 0\) admet pour vecteur directeur \(\overrightarrow u \left( { - \beta \,;\alpha } \right)\) et pour vecteur normal \(\overrightarrow v \left( { \alpha \,;\beta } \right)\).
Cercle
L’orthogonalité permet de définir un cercle. Soit \(A\) et \(B\) deux points distincts. Le cercle de diamètre \([AB]\) est l’ensemble des points \(M\) vérifiant \(\overrightarrow {MA} .\overrightarrow {MB} = 0\)
La tangente d’un cercle de centre \(O\) au point \(M\) est l’ensemble des points \(P\) qui vérifient \(\overrightarrow {MP} .\overrightarrow {MO} = 0\)
Exercice
Soit un carré \(ABCD\) avec \(M\) milieu de \([BC],\) \(N\) milieu de \([AB]\) et \(P\) un point de la droite \((CD)\) tel que \(CP = \frac{1}{4}CD.\) Soit \(I\) l’intersection des droites \((AM)\) et \((NP).\) Les droites \((BI)\) et \((CI)\) sont-elles perpendiculaires ?
Corrigé
Commençons par tracer une représentation graphique pour se fixer les idées.
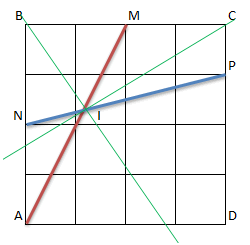
Premier réflexe, considérer ce carré quadrillé comme un repère orthonormé d’origine \(A.\) Ainsi, nous avons \(M(2\,;4),\) \(P(4\,;3),\) etc.
Il faut bien sûr trouver les coordonnées de \(I.\) C’est l’intersection de deux droites représentatives d’une fonction linéaire d’équation \(y = 2x\) et d’une fonction affine d’équation \(y = 0,25x + 2.\) Ce type d’exercice est fréquemment réalisé en classe de seconde. Posons le système :
\(\left\{ {\begin{array}{*{20}{c}} {y = 2x}\\ {y = 0,25x + 2} \end{array}} \right.\)
On trouve \(I\left( {\frac{8}{7};\frac{{16}}{7}} \right)\)
Passons aux vecteurs. Leur détermination relève là aussi du programme de seconde (voir page vecteurs et coordonnées). On obtient :
\(\overrightarrow {BI} \left( {\begin{array}{*{20}{c}} {\frac{8}{7}}\\ { - \frac{{12}}{7}} \end{array}} \right)\) et \(\overrightarrow {CI} \left( {\begin{array}{*{20}{c}} { - \frac{{20}}{7}}\\ { - \frac{{12}}{7}} \end{array}} \right)\)
Le repère étant orthonormé, nous utilisons, comme dans l'exercice précédent, la formule \(xx’ + yy’.\) Ce qui nous donne \(\overrightarrow {BI} .\overrightarrow {CI} = - \frac{{16}}{7}\)
Le produit scalaire n’est pas nul. Les droites \((BI)\) et \((CI)\) ne sont donc pas perpendiculaires (tant pis pour elles).
Voir aussi l'exercice 2 de la page sur le produit scalaire avec coordonnées.
