Produit scalaire : la formule du cosinus
En France, le produit scalaire est découvert en classe de première générale et des premières STI2D et STL. Comme il s’agit d’une notion assez difficile à appréhender, vous en trouverez ici une initiation très progressive.
Problématique par l’exemple
Soit un objet qui se déplace sur un rail, par exemple un train miniature. Pour le faire avancer sur une distance donnée, il faut le tirer avec un bâton dont l'extrémité peut être accrochée n’importe où autour de la locomotive.
Selon l’endroit où le bâton est fixé, le travail réalisé ne sera pas le même.
Si l’on tire la locomotive dans le sens du rail, elle avance parfaitement bien. Le travail fourni est maximum.
Si l’on tire sur le côté, perpendiculairement au rail, le travail est nul. Le train n’avance pas. Il peut juste dérailler !
Si l’on pousse la locomotive par devant au lieu de la tirer, le train recule (travail "résistant").
Si l’on tire la locomotive sur le côté mais pas perpendiculairement au rail, c’est-à-dire que le train et le bâton forment un angle qui n’est ni droit ni plat, la locomotive avance, mais moins bien que dans notre premier cas de figure. Vous l’avez deviné, le travail réalisé dépend de l’angle formé par le bâton et le rail.

Les manuels de maths comportent souvent des exercices de physique de ce type. La distance parcourue est exprimée en mètres, l’intensité de la force en newtons et le travail en joules. Quel rapport avec les maths ? La distance et la force sont représentées par des vecteurs. Le travail est obtenu par un produit scalaire. Il dépend des deux vecteurs et de l’angle qui existe entre eux.
Un produit scalaire s'exprime donc sous la forme d'un réel.
Expression
Ceci nous amène à la formule, ou plutôt à l’une d’elles puisqu’il en existe plusieurs (voir le produit scalaire dans le plan). Mais auparavant, un petit rappel sur la norme d’un vecteur :
Soit \(\overrightarrow u \left( {\begin{array}{*{20}{c}} x\\ y \end{array}} \right)\) alors \(\| {\overrightarrow u } \| = \sqrt {{x^2} + {y^2}} \)
C’est la distance euclidienne vue en seconde (voir la géométrie analytique), évidemment positive.

Bref, la formule. Le produit scalaire fait intervenir le cosinus de l’angle :
\[\overrightarrow u .\overrightarrow v = \| {\overrightarrow u } \| \times \| {\overrightarrow v } \| \times \cos \left( {\overrightarrow u ,\overrightarrow v } \right)\]
Bien sûr, si les vecteurs sont orthogonaux, le cosinus est égal à 0 (soit \(\cos \left( {\frac{\pi }{2}} \right)\)) et donc le produit scalaire est nul.
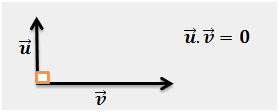
Pour utiliser cette propriété, vous pouvez faire l'exercice sur l'orthogonalité.
Le produit scalaire est donc du signe du cosinus, c’est-à-dire positif si l’angle formé par les vecteurs est aigu et négatif si l’angle est obtus (à visualiser sur le cercle trigonométrique).
Pour calculer la mesure d'un angle \(\widehat {AOB}\) ou pour déterminer l'une des distances \(OA\) ou \(OB\), on utilise donc la relation :
\[\overrightarrow {OA} .\overrightarrow {OB} = OA \times OB \times \cos \widehat {AOB}\]
Si nos deux vecteurs sont colinéaires et de même sens, le cosinus est égal à 1 et nous avons \(\overrightarrow u .\overrightarrow v = \| {\overrightarrow u } \| \times \| {\overrightarrow v } \|\)
S’ils sont colinéaires et de sens contraire, l’égalité devient \(\overrightarrow u .\overrightarrow v = -\| {\overrightarrow u } \| \times \| {\overrightarrow v } \|\)
Si les deux vecteurs sont égaux, on parle de carré scalaire.
Précisons enfin que la multiplication scalaire est commutative : \(\overrightarrow u .\overrightarrow v = \overrightarrow v .\overrightarrow u \)
Exemple :
Ci-dessous, un carreau vaut 1 unité.
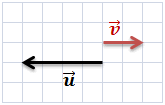
Les vecteurs sont colinéaires mais de sens contraire. Le produit scalaire est donc égal à \(-4 \times 2 = -8.\)
Passons à de petites applications simples. Lorsque vous en aurez appris davanatge sur le sujet, vous pourrez vous exercer sur des problématiques plus intéressantes (voir par exemple la page produit scalaire et mesures d'angles).
Exercices
1- Que signifie l’expression \(\overrightarrow u .\overrightarrow v .\overrightarrow w \) ?
2- Calculer le produit scalaire\(\overrightarrow u .\overrightarrow v \)à partir des données suivantes :
\(\| {\overrightarrow u } \| = 2\), \(\| {\overrightarrow v } \| = \frac{{\sqrt 3 }}{3}\) et \(\left( {\overrightarrow u ,\overrightarrow v } \right) = \frac{\pi }{6}\)
Voir aussi les exercices sur le produit scalaire.
Corrigés
1- Rien ! Seuls deux vecteurs peuvent intervenir. On pourrait à la rigueur ajouter des parenthèses à l’expression, ce qui se traduirait par un scalaire que multiplie un vecteur ; mais le résultat serait un vecteur et non un réel.
2- En principe, vous savez que \(\cos \frac{\pi }{6} = \frac{{\sqrt 3 }}{2}\)
Il suffit d’appliquer la formule du cosinus.
\(2 \times \frac{\sqrt{3}}{3} \times \frac{\sqrt{3}}{2} = 1.\)
D’une façon générale, lorsqu’on connaît les longueurs et l’angle formé par les vecteurs, c’est la formule indiquée sur cette page qu’il faut utiliser. Sinon, on se tourne vers la formule du projeté, la formule des normes ou d'autres...
