Exercices de limites avec FI
C'est un jeu (enfin non, un exercice) auquel s'adonnent les élèves de terminale en maths de spécialité : découvrir une limite de fonction dont l'expression nécessite de recourir à quelques subtilités.
En effet, les limites de fonctions usuelles sont bien connues. Quant aux opérations sur fonctions usuelles et aux composées de fonctions, leurs limites sont souvent simples à déterminer. Mais parfois, il y a un os que l'on appelle forme indéterminée (FI). Par exemple, lorsqu'on arrive à une somme entre \(+∞\) et \(-∞\), qui l'emportera ? \(+ ∞,\) \(-∞\) ou un réel ?

Les quatre exercices qui suivent illustrent quatre situations classiques. Donc des savoir-faire à maîtriser. Ensuite, vous pourrez passer aux exercices sur limites avec exponentielles et aux exercices sur limites avec racines carrées.
Exercice 1
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = x^2 - 2x + 5\)
Déterminer \(\mathop {\lim }\limits_{x \to + \infty } f(x)\)
Corrigé expliqué
C'est le cas d'indétermination le plus simple. Elle est de type somme \(+∞ - ∞.\)
L'astuce consiste à factoriser le polynôme par le monôme de degré le plus élevé. Ici, \(x^2.\) C'est un tour de passe-passe que vous n'avez peut-être pas encore pratiqué : la factorisation de 5 par \(x^2\) ne saute pas aux yeux !
Voici donc ce qu'il faut chercher :
\(\mathop {\lim }\limits_{x \to + \infty } {x^2}\left( {1 - \frac{2}{x} + \frac{5}{{{x^2}}}} \right)\)
Nous obtenons un produit de fonctions. La limite de \(x^2\) est bien sûr \(+∞.\) Quant à la seconde, la limite à \(+∞\) est 1. Pourquoi ? Parce que c'est la somme de 1 et de deux limites égales à 0 (voir les limites de la fonction inverse).
Au total, nous multiplions \(+∞\) par 1 qui est un nombre positif. Donc, par produit, \(\mathop {\lim }\limits_{x \to + \infty } f(x) = + \infty .\)
Notez qu'à une époque les limites étaient au programme de terminale ES (économique et sociale). Dans un cas comme celui-ci, il suffisait d'apporter comme explication « en \(+∞\) un polynôme se comporte comme son terme de plus haut degré ». Dans vos évaluations, ce type d'explication risque de ne pas suffire mais au moins retenez le principe !
Exercice 2
Soit la fonction \(f\) définie par \(f(x) = \frac{3x + 1}{x^2 + 2x - 8}\)
Déterminer \(\mathop {\lim }\limits_{x \to - \infty } f(x)\)
Corrigé expliqué
Nous voici en présence d'une forme indéterminée de type \(\frac{-∞}{+∞}.\) Que faire ?
Il faut factoriser le numérateur et le dénominateur par le monôme du plus haut degré.
\(\frac{3x + 1}{x^2 + 2x - 8} = \frac{3x(1+\frac{1}{3x})}{x^2(1 + \frac{2}{x}-\frac{8}{x^2})}\)
…que l'on peut écrire :
\[\frac{3}{x} × \frac{1+\frac{1}{3x}}{1 + \frac{2}{x} -\frac{8}{x^2}}\]
La limite à l'inifini du premier facteur est bien sûr 0. Celle du second facteur est 1. Donc, par produit, \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 0\)
Là encore, vous pouvez vous souvenir d'une astuce pour vérifier votre résultat : à l'infini, une fonction rationnelle se comporte comme le quotient des termes de plus haut degré. Ainsi \(\mathop {\lim }\limits_{x \to - \infty } f(x)\) \(=\) \(\mathop {\lim }\limits_{x \to - \infty } \frac{3x}{x^2}\) \(=\) \(\mathop {\lim }\limits_{x \to - \infty } \frac{3}{x}\) \(=\) \(0^-\)
Exercice 3
Soit la fonction \(f\) définie sur \(\mathbb{R} \backslash \{-4\, ;-2\}\) par \(f(x) = -\frac{x^2 + x - 2}{2x^2 + 12x + 16}\)
Déterminer \(\mathop {\lim }\limits_{x \to - 2 } f(x)\)
Corrigé expliqué
Nous ne cherchons pas une limite à l'infini, donc la technique précédente ne s'applique pas.
Si l'on remplace \(x\) par -2, on obtient une fraction de type \(\frac{0}{0}\) d'où une limite indéterminée.
En théorie, lorsqu'une limite en un réel \(α\) se traduit par une indétermination de type \(\frac{0}{0}\) on factorise numérateur et dénominateur par la plus grande puissance de \(x - α.\)
Concrètement, vous devez factoriser le numérateur et le dénominateur après avoir calculé leurs discriminants.
En l'occurrence, vous trouvez \(Δ = 9\) au numérateur et \(Δ = 16\) au dénominateur. On peut donc exprimer \(f\) ainsi : \(f(x) = \frac{(x + 2)(x - 1)}{-2(x + 2)(x + 4)}\) \(=\) \(\frac{x - 1}{-2x - 8}\)
Et là les choses deviennent plus simples.
\(\mathop {\lim }\limits_{x \to - 2 } \frac{x - 1}{-2x - 8} = \frac{3}{4}\)
Attention, lorsqu'on trace la courbe représentative de \(f\) il ne saute pas aux yeux que celle-ci n'est pas définie en -2 ! Tout dépend du logiciel. Avec la calculatrice TI-83 Premium CE, en regardant bien on remarque un « trou » :
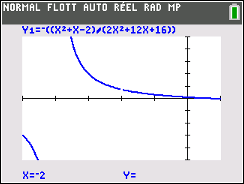
Exercice 4
Soit la fonction \(f\) définie sur \([0\ ; 16[ ∪]16\, ;+∞[\) par \(f(x) = \frac{\sqrt{x} - 4}{x - 16}\)
Déterminer \(\mathop {\lim }\limits_{x \to 16 } f(x)\)
Corrigé expliqué
La limite est de type \(\frac{0}{0}\)
Avec la technique des quantités conjuguées faisons apparaître une même expression au numérateur et au dénominateur.
\(f(x) = \frac{\sqrt{x} - 4}{(\sqrt{x} - 4)(\sqrt{x} + 4)}\)
Il ne reste qu'à simplifier l'expression.
\(f(x) = \frac{1}{\sqrt{x} + 4}\)
Dès lors, le calcul de la limite ne pose plus de difficulté.
\(\mathop {\lim }\limits_{x \to 16 } f(x) = \frac{1}{8}\)
Victoire.
