Limites indéterminées avec fonction exp
Vous souhaitez vous perfectionner à la détermination de limites. Plus précisément, vous vous êtes déjà exercé avec les formes indéterminées et vous souhaitez poursuivre avec un entraînement de plus haut niveau.
Pour mener à bien cette louable entreprise, voici quelques exercices corrigés avec fonction exponentielle.
Échauffement
Déterminer la limite en \(+ ∞\) de la fonction \(f\) définie sur \(\mathbb{R}\) comme suit :
\(f(x) = e^x + e^{-x}\)
Corrigé
Ce n'est même pas une forme indéterminée !
\(\mathop {\lim }\limits_{x \to + \infty } {e^x} = + \infty \) et \(\mathop {\lim }\limits_{x \to + \infty } {e^{ - x}} = 0\)
Donc, par somme, \(\mathop {\lim }\limits_{x \to + \infty } {f(x)} = + \infty \)

Exercice 1
Déterminer la limite en \(+ ∞\) de la fonction \(f\) définie comme suit :
\(f(x) = \frac{2e^x + 1}{e^x – 2}\)
Corrigé
Nous sommes en présence d'une forme indéterminée de type « \(\frac{∞}{∞}\) ». L'astuce consiste à factoriser le numérateur et le dénominateur par \(e^x.\)
\(f(x) = \frac{e^x(2 + \frac{1}{e^x})}{e^x(1 - \frac{2}{e^x})}\)
\(⇔ f(x) = \frac{2 + \frac{1}{e^x}}{1 - \frac{2}{e^x}}\)
À présent, il est aisé de déterminer la limite…
\(\mathop {\lim }\limits_{x \to + \infty } \left( {2 + \frac{1}{x}} \right) = 2\) et \(\mathop {\lim }\limits_{x \to + \infty } \left( {1 - \frac{2}{x}} \right) = 1\)
Donc, par quotient, \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 2.\)
Note : si cette fonction devait modéliser une situation concrète, on s'intéresserait certainement à la « vitesse » à laquelle elle s'approche de 2. Ici, ce serait très rapide. Ci-dessous, la fenêtre de calculatrice indique une valeur de 2,0016784 pour \(x = 8.\)
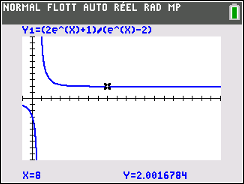
Exercice 2
Déterminer la limite en \(- ∞\) de la fonction \(f\) définie comme suit :
\(f(x) = e^x(2 - x)\)
Corrigé
Forme indéterminée de type « \(0 × ∞\) »
Développons.
\(f(x) = 2e^x - xe^x\)
\(\mathop {\lim }\limits_{x \to - \infty } 2{e^x} = 0\)
D'après les croissances comparées, \(\mathop {\lim }\limits_{x \to - \infty } x{e^x} = 0\)
Donc, par différence, \(\mathop {\lim }\limits_{x \to - \infty } f(x) = 0\)
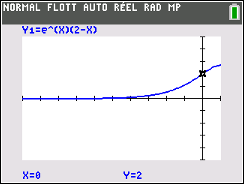
Exercice3
Déterminer la limite en \(+ ∞\) de la fonction \(f\) définie comme suit :
\(f(x) = \frac{(x + 3)^2}{e^x}\)
Corrigé
C'est une forme indéterminée de type \(\frac{∞}{∞}\)
Comme vous l'avez remarqué, pour faire les choses dans les règles, on commence toujours par factoriser.
\(f(x) = \frac{[x(1 + \frac{1}{x})]^2}{e^x}\)
\(\Leftrightarrow f(x) = \frac{x^2}{e^x} × \frac{(1 + \frac{1}{x})^2}{e^x}\)
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{{x^2}}}{{{e^x}}} = 0\) d'après les croissances comparées.
\(\mathop {\lim }\limits_{x \to + \infty } {\left( {1 + \frac{1}{x}} \right)^2} = 1\) donc, par quotient :
\(\mathop {\lim }\limits_{x \to + \infty } \frac{{{{\left( {1 + \frac{1}{x}} \right)}^2}}}{{{e^x}}} = 0\)
D'où, par produit, \(\mathop {\lim }\limits_{x \to + \infty } f(x) = 0\)
Comme vous le constatez, il n'est pas si difficile de « cracker » une limite puisqu'on utilise toujours la même ruse (la factorisation). Vous pouvez aussi tracer la courbe représentative de la fonction avec une calculatrice pour conjecturer quelle est la limite cherchée, étant entendu que c'est une aide et non une preuve !
