Fonction exponentielle de base e
Cette page a été rédigée pour les élèves de première générale puisque, depuis la rentrée 2019, c'est en première que l'on aborde les exponentielles.
Présentation générale
Définition : la fonction exponentielle est l'unique fonction dérivable sur \(\mathbb{R}\) qui est égale à sa dérivée et par laquelle l'image de 0 est 1 (démonstration en page unicité de la fonction exp). Elle est notée « exp ».

Elle est définie sur \(\mathbb{R}\) par \(f(x) = e^x,\) \(e\) étant environ égal au réel 2,7182818 (nombre irrationnel). Ainsi, \(\exp(1) = e\) et \(\exp (x) = e^x.\)
La fonction \(\exp\) est strictement positive et croissante sur \(\mathbb{R}.\)
Ainsi, pour tous réels \(a\) et \(b\), \(e^a < e^b \Leftrightarrow a < b.\)
Sa courbe représentative est la suivante (réalisée avec GeoGebra).
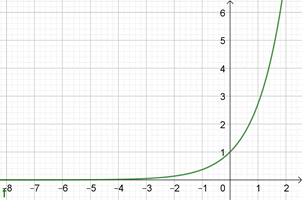
Nous avons vu que la dérivée de la fonction exponentielle s'écrit tout simplement \(f'(x) = e^x.\) Soit maintenant la fonction \(f:x \mapsto e^{u(x)}.\) Sa dérivée \(f’\) est définie par \(f’(x) = u’(x)e^{u(x)}\) (programme de terminale). La dérivée de l'exponentielle d'une fonction affine \(f:x\mapsto e^{ax + b}\) s'écrit donc \(f'(x) = ae^{ax + b}\) (programme de première). Applications en page d'exercices de dérivation avec exponentielles (niveau terminale).
Il existe un lien entre cette fonction et les suites géométriques (voir la croissance exponentielle).
Propriétés
La fonction exponentielle est une fonction exponentielle de base \(a\) particulière. Ses propriétés sont celles des calculs de puissance.
Il est donc évident que \(e^0 = 1\) puisque tout réel strictement positif à la puissance 0 est égal à 1.
Ainsi, \(e^a \times e^b = e^{a + b}.\)
Il s'ensuit que pour tout réel \(x\) nous avons \(e^x \times e^{-x} = 1.\)
De même, \(\frac{e^a}{e^b} = e^{a - b}\) (\(a\) et \(b \in \mathbb{R}\))
Par exemple, \(\frac{e^{2,25}}{e^{1,25}} = e^{2,25} - e^{1,25}\) \(= e^1 = e\)
Retenez aussi que \(\frac{1}{e^x} = e^{-x}\)
Comme une racine carrée est une puissance 0,5, on peut aussi remarquer que \(\sqrt {{e^x}} = {e^{\frac{x}{2}}}\)
Enfin, pour tout \(n \in \mathbb{Z}\) nous avons l'égalité \(e^{nx} = {\left( {{e^x}} \right)^n}\)
Vous pouvez vous entraîner en page d'exercices sur les propriétés de l'exponentielle.
Exemple d'équation
\(e^{x+3} = 1\)
Quand ce cas se présente, vous devez tout de suite penser que \(1 = e^0.\) Une équation ou une inéquation avec exponentielle doit toujours être transformée pour avoir les deux membres sous forme d'exponentielles.
Donc \(e^{x+3} = e^0\)
Là, vous laissez tomber les exponentielles en pécisant que la fonction exponentielle est strictement croissante (il serait faux de procéder ainsi avec des carrés puisque la fonction carré n'est pas strictement croissante ; il est donc recommandé de préciser pourquoi on se permet d'évacuer les exponentielles comme des malpropres).
\(x + 3 = 0\) donc \(x = -3\)
Des exercices se trouvent en page d'équations avec exponentielle. Voir également les inéquations avec exponentielle.
Exemple de détermination du sens de variation
Soit la fonction \(f\) définie sur \(\mathbb{R} \backslash \{0\}\) par \(f(x) = \frac{e^x}{x}\)
Dérivons d’abord \(f\) (bien qu’il soit tout à fait possible de déterminer son sens de variation sans passer par cette étape). Voir la formule de la dérivé d’un quotient de fonctions \(\frac{u(x)}{v(x)}\) avec \(u(x) = e^x,\) \(u’(x) = e^x,\) \(v(x) = x\) et \(v’(x) = 1.\)
\[f'(x) = \frac{{x{e^x} - {e^x}}}{{{x^2}}} = {e^x} \times \frac{{x - 1}}{{{x^2}}}\]
Pour tout \(x,\) \(e^x > 0\) et \(x^2 \geqslant 0.\) Donc, le signe de \(f'\) est le signe de \((x - 1).\) Par conséquent, les variations de \(f\) sont les suivantes (Cf. lien entre fonction et dérivée) :
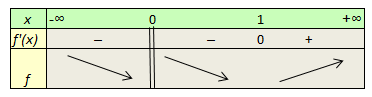
Autre exemple
Sans utiliser la dérivée, exemple tiré de l’épreuve du bac ES, Amérique du Nord, juin 2007.
Soit l’intervalle \(J = ]0,5\,;+\infty[\) et \(f\) une fonction définie sur \(J\) par :
\[f(x) = ({x^2} - x + 1){e^{2x - 1}}\]
Déterminons le signe de chacun des deux facteurs.
Quel est le signe du trinôme \((x^2 - x + 1)\) ? Calculons le discriminant.
\(\Delta = (-1)^2 - 4 \times 1 \times 1 = -3\)
Comme \(\Delta < 0,\) le signe du trinôme est celui de \(a = 1,\) c’est-à-dire positif.
Par ailleurs, la fonction \(\exp\) est strictement positive.
Un produit de facteurs positifs étant positif, il est limpide que \(f\) est strictement positive.
