Formes d'écriture des fonctions du second degré
Le texte qui suit est destiné aux élèves qui commencent leur année de première. Ce point du programme est une synthèse de plusieurs thèmes abordés en seconde (fonction carré, factorisation, tableau de variation, inéquations…), qui comprend en outre la forme canonique.
Plusieurs expressions
L’expression d’une fonction du second degré contient une variable \(x\) élevée à la puissance 2 et éventuellement aussi à la puissance 1, à l’exclusion de toute autre expression de \(x.\) Elle peut s’écrire sous plusieurs formes. La plus facilement identifiable est la forme développée, de type \(f(x) = ax^2 + bx + c\), avec \(b\) et \(c\) réels et \(a\) un réel non nul.
Une autre écriture est la forme canonique : \(f(x) = a(x - \alpha)^2 + \beta\) avec \(\alpha\) et \(\beta\) appartenant à l'ensemble des réels.
Enfin, il existe une forme factorisée mais toutes les fonctions du second degré ne sont pas factorisables.
Au début de l'année de première, les exercices consistent d’abord à IDENTIFIER une fonction du second degré. Il faut alors développer puis réduire l’expression de l’énoncé pour vérifier qu'elle s’écrit bien sous la forme \(ax^2 + bx + c.\)
Exemple : \(f(x) = (x + 2)^2 - (x - 3)^2\)
Développons les deux identités remarquables : \(x^2 + 4x + 4 - (x^2 - 6x + 9)\) \(= 10x - 5\)
Contrairement aux apparences, ce n’était pas une fonction du second degré mais une fonction affine (bien déguisée).
Autre exemple : \(g(x) = x + \frac{x^2}{4}.\) Il s’agit bien cette fois d’une fonction du second degré, avec \(a = \frac{1}{4},\) \(b = 1\) et \(c = 0.\)
À chaque forme son utilité
Un exercice habituel est la recherche de l’extremum. On parle alors du sommet de la courbe. Terme très curieux puisque si \(a\) est positif, le sommet est le point le plus bas.
En effet, une fonction du second degré se traduit graphiquement par une parabole dont il faut trouver le point de retournement (un minimum si \(a > 0\) ou un maximum si \(a < 0.\) Si l’on dispose de la forme canonique c’est tant mieux car c’est la plus pratique pour connaître l’emplacement du point en question. Les coordonnées de l'extremum sont \((\alpha\, ;\beta)\).
La forme développée est quant à elle la plus indiquée pour connaître rapidement \(f(0),\) c’est-à-dire là où la courbe croisee l’axe des ordonnées, puisqu’il s’agit fort logiquement de \(c.\) C’est aussi la plus pratique pour déterminer la plupart des points de la courbe lorsqu’on a oublié sa calculatrice.
Enfin, la forme factorisée permet de trouver sans mal le ou les deux points pour lesquels \(f(x) = 0,\) là où la courbe croise l’axe des abscisses (un produit de facteurs est nul si l’un des facteurs est nul). Mais toutes les paraboles ne croisent pas cet axe. C’est lié au fait que la forme factorisée n’existe pas pour toutes les fonctions du second degré.

Application
Soit les fonctions \(f\) et \(g\) définies sur \(\mathbb{R}\) par \(f(x) = (x + 2)^2 - 9\) et \(g(x) = (x + 5)(x - 1).\)
Montrer que \(f\) et \(g\) ne font qu’une seule et unique fonction. Résoudre sans calculatrice \(f(x) = 0,\) puis calculer \(f(0)\) et les coordonnées de l’extremum.
Corrigé : cet exercice est assez classique et somme toute très simple. Il faut juste penser à une chose : lorsqu’on cherche à montrer que deux expressions de fonctions sont identiques, il faut déterminer de laquelle on part pour arriver à l’autre. Mais si l’on ne sait pas par laquelle commencer, on peut modifier les deux pour arriver à une troisième. La plupart du temps, il est plus simple de développer. Donc développons \(f\) et \(g\) pour constater que le résultat est le même. Allons-y.
\(f(x) = x^2 + 4x + 4 - 9\) \(= x^2 + 4x - 5\)
\(g(x) = x^2 - x + 5x - 5\) \(= x^2 + 4x - 5\)
Ô joie ! Nous arrivons au même résultat. Donc, \(f\) et \(g\) ne font qu'une !
Pour résoudre \(f(x) = 0,\) le plus simple consiste à prendre la forme factorisée. Il apparaît aussitôt que les solutions sont \(\{-5\,;1\}.\) Pour connaître \(f(0),\) il suffit de prendre la forme développée. Donc \(f(0) = -5.\) Enfin, l’extremum est un minimum puisque la forme développée nous indique \(a = 1\) (nombre positif). Ses coordonnées sont \((-2\,;-9).\) La forme canonique nous les donne directement.
Notez qu’il n’est pas nécessaire de disposer des trois formes pour répondre aux questions. Simplement, la recherche risque d’être moins immédiate. Par exemple si les solutions de \(f(x) = 0\) sont -5 et 1, il suffit de faire leur moyenne (donc \(\frac{-5 + 1}{2} = -2\)) pour obtenir l’abscisse du minimum puis de déterminer l’image de cette valeur pour obtenir son ordonnée.
Ci-dessous apparaît sous nos yeux ébahis la parabole, réalisée sur Sine Qua Non. Tous les résultats ci-dessus sont bien visibles :
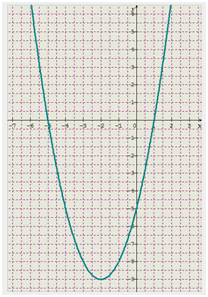
Note : les calculs de minimum ou de maximum par la calculatrice ne sont pas très utiles, d’autant qu’ils ne sont pas réalisés sur l’ensemble de définition mais sur un intervalle à définir.
Quiz graphique
Voici trois courbes et trois expressions de fonctions.
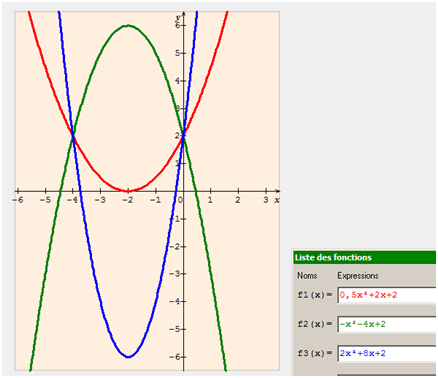
Auriez-vous su affecter les bonnes expressions aux bonnes courbes ? C’est possible en ne s’intéressant qu’au coefficient \(a\) (donc devant \(x^2.\)) La courbe verte est la plus facile à identifier puisqu’elle est la seule à monter puis à descendre. \(a\) est donc négatif. La courbe rouge est beaucoup plus évasée que la bleue, très serrée. \(a\) est donc beaucoup plus petit (en l’occurrence, 0,5).
