Démonstrations de l'unicité d'une fonction où \(f(0) = 1\) et \(f = f'\)
Voici une démonstration autrefois exigible au programme de terminale S, au chapitre fonction exponentielle. Nous allons prouver qu'une unique fonction \(f\) définie et dérivable sur \(\mathbb{R}\) a pour propriétés \(f(0) = 1\) et \(f = f'.\) Nous admettrons qu'elle existe.
Avant de se lancer dans la démonstration proprement dite, il faut prouver que cette fonction ne peut pas être nulle. Nous nous servirons ensuite de ce premier résultat.
Elle n'est pas nulle !
Soit une fonction \(h\) définie sur \(\mathbb{R}\) par \(h(x) = f(x)f(-x).\)
\(h\) est dérivable sur \(\mathbb{R}\) puisque \(f(x)\) et \(f(-x)\) le sont.
Dérivons ce produit de fonctions.
\((h'(x) = f(x)(-f'(-x)) + f'(x)f(-x)\)
\(\Leftrightarrow h'(x) = -f(x)(f'(-x)) + f'(x)(f(-x))\)
Or, nous avons supposé que \(f(x) = f'(x).\)
\(h'(x) = -f(x)(f(-x)) + f(x)(f(-x)).\) D'où \(h'(x) = 0.\)
Donc \(h\) est une fonction constante, mais rien ne nous dit qu'elle n'est pas nulle…
Sauf que nous savons que \(f(0) = 1\) et donc que \(h(0) = 1.\) Il s'ensuit que \(h\) est une fonction constante égale à 1.
Si vous avez déjà étudié les propriétés de l'exponentielle, cela doit vous paraître évident : nous avons prouvé que \(e^x \times e^{-x} = e^0 =.\)
Démonstration d'unicité
Supposons qu'il existe deux fonctions \(f\) et \(g\) pour lesquelles \(f(0) = 1\) et \(g(0) = 1\) et pour lesquelles \(f(x) = f'(x)\) et \(g(x) = g'(x).\) Si l'on prouve que \(f = g,\) alors on prouve l'unicité de la fonction.
Pour démontrer que \(f = g,\) on établit que \(\frac{f}{g}\) (ou \(\frac{g}{f}\)) \(= 1.\)
Bien sûr, le dénominateur ne doit pas être nul. Et pour notre plus grande satisfaction il ne l'est pas. C'est ce que nous avons démontré précédemment.
Donc, pour établir que \(\frac{f}{g} = 1,\) nous allons reprendre la même démarche : prouver que la fonction est constante en montrant que sa dérivée est nulle, puis calculer sa valeur en 0.
Dérivée d'une fonction quotient : \(\left(\frac{f(x)}{g(x)}\right)'\) \(=\) \(\frac{f(x)g'(x) - f'(x)g(x)}{g^2(x)}\)
Par hypothèse, \(f = f'\) et \(g = g'\) donc \(\frac{f(x)g'(x) - f'(x)g(x)}{g^2(x)} = 0\)
Une bonne chose de faite ! Et maintenant que l'on sait que \(\frac{f}{g}\) est constante, on calcule \(\frac{f(0)}{g(0)}.\) Le calcul est rapide : \(\frac{1}{1} = 1.\)
Donc \(f = g,\) la fonction pour laquelle \(f = f'\) sur \(\mathbb{R}\) et pour laquelle \(f(0) = 1\) est unique !
Autre démonstration
Une démonstration alternative, pour le plaisir (mais si, mais si).
Supposons encore qu'il existe deux fonctions \(f\) et \(g\) pour lesquelles \(f(0) = 1\) et \(g(0) = 1\) et pour lesquelles \(f(x) = f'(x)\) et \(g(x) = g'(x).\)
Soit \(h(x) = f(x) × g(-x).\)
Prouvons là encore que \(h\) est constante.
\(h'(x) = f(x)(-g'(-x)) + f'(x)g(-x).\)
Si vous avez encore en tête la première démonstration, vous pouvez actionner le pilotage automatique…
\(h'(x) = -f(x)(g(-x)) + f(x)g(-x) = 0.\)
Ainsi \(h\) est constante. Comme \(f(0) = g(0) = 1,\) alors \(h(x) = 1.\)
Donc \(h(x) = f(x) × g(-x) = 1\) et notre première démonstration nous avait appris que \(f(x) \times f(-x) = 1.\)
Il s'ensuit que \(f(x) × g(-x) = f(x) × f(-x).\)
On peut diviser les deux membres de l'égalité par \(f(x)\) puisque \(f\) n'est jamais nulle.
Ainsi \(g(-x) = f(-x)\) et donc \(f = g.\) La fonction pour laquelle \(f = f'\) sur \(\mathbb{R}\) et pour laquelle \(f(0) = 1\) est unique (et la démonstration ne l'est pas !).
Conséquences : positivité et croissance de la fonction exponentielle
Pour montrer la positivité, pas besoin de longs calculs. Nous savons que cette fonction est dérivable sur R. Elle est donc continue sur \(\mathbb{R}.\) Nous avons démontré qu'elle n'est jamais nulle. Elle est donc soit strictement positive soit strictement négative. Or \(e^0 = 1.\) Donc la fonction exponentielle est strictement positive (application du TVI).
Pas besoin non plus de grands développements pour montrer qu'elle est croissante : nous savons que la fonction exponentielle est égale à sa dérivée sur \(\mathbb{R}.\) Nous venons de montrer que la fonction est positive. Donc sa dérivée l'est aussi. Et si \(f' > 0,\) alors \(f\) est croissante. Vous voyez que ce n'est pas difficile !
Annexe
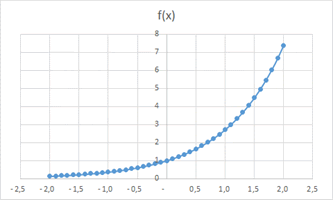
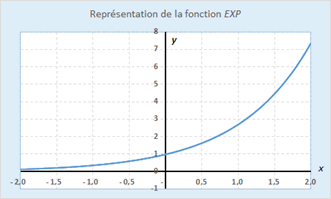
Afin de visualiser une partie de ce que nous avons démontré, traçons la courbe représentative de la fonction exponentielle. Nous verrons alors qu'elle est continue, strictement positive et croissante (au moins sur l'intervalle du tracé) et que \(f(0) = 1.\) Vous devinerez facilement quelles sont ses limites.
Pour ajouter une certaine originalité, elle ne sera pas tracée avec une calculatrice graphique ou avec un logiciel de mathématiques. Ce serait trop simple. Nous le ferons avec Excel.
Nous nous contenterons de l'intervalle \([-2\,; 2].\) Dans la colonne A, nous entrons les valeurs de \(x\) avec un pas de 0,1. C'est-à-dire qu'il faut entrer -2 et, sur la ligne suivante, la référence à la cellule du dessus +0,1. Sélection de cette cellule puis cliquer-glisser vers le bas. En colonne B, il suffit d'entrer la fonction EXP avec la référence à la cellule de gauche et de cliquer-glisser vers le bas.
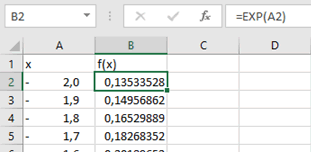
Ensuite, sélectionner la plage de valeurs, intitulés compris, et cliquez sur Insérer puis, dans le choix de graphiques proposés, sélectionner l'icône qui représente un nuage de points. Dans le sous-menu, choisissez le deuxième où les points sont reliés par des courbes. Vous obtenez alors un graphe pas très joli (le premier ci-dessous) mais vous pouvez toujours le customiser pour améliorer son esthétique (le second).