Dérivée de type (u × v) et nombre dérivé avec TI-82
Les deux exercices qui suivent s’inscrivent dans un programme de maths de première générale. Ils sont plutôt faciles.
Rappels
Rappel de la formule de dérivation d'une fonction produit :
La dérivée d'une fonction \(f\) pouvant s'écrire \(f(x) = u(x) × v(x)\) est \(f'(x) = u’(x)v(x) + u(x)v’(x),\) que l’on simplifie abusivement par \(u’v + uv’.\)
Prérequis pour les exercices : les dérivées d’une fonction du second degré et de degré 3 sont supposées connues, ainsi que celle de la fonction racine carrée qui est, rappelons-le, \(f'(x) = \frac{1}{2\sqrt{x}}.\)
Exercice 1
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x)\) \(= (x + 2)(x^2 - 2x + 1)\)
Déterminer une expression de sa dérivée \(f’(x)\) de deux façons différentes.
Exercice 2
Soit \(g\) la fonction définie sur \(\mathbb{R}_+\) par \(g(x)\) \(= \sqrt{x}(2x - 5)\)
Établir sa dérivée \(g’(x)\) puis calculer \(g’(1).\) Vérifier le résultat à la calculatrice.

Corrigé 1
La première façon de dériver \(f\) consiste à la présenter sous forme développée avant de la dériver.
\(f(x) = x^3 - 2x^2 + x + 2x^2 - 4x + 2\)
\(\Leftrightarrow f(x) = x^3 - 3x + 2\)
Il est à présent très simple de dériver ce polynôme…
\(f’(x) = 3x^2 - 3\)
Cette façon de procéder est très rapide mais elle illustre hélas bien mal le thème de la dérivation d’un produit de fonctions.
La seconde manière consiste à utiliser la formule du produit de fonctions.
Nous avons \(u(x) = x + 2\) et donc \(u’(x) = 1.\) De même, \(v(x) = x^2 - 2x + 1\) ce qui implique bien sûr \(v’(x) = 2x - 2.\)
Appliquons la formule : \(f’(x)\) \(= 1(x^2 - 2x + 1) + (x + 2)(2x - 2)\)
Développons tout ce joli monde.
\(f’(x) = x^2 - 2x + 1 + 2x^2 - 2x + 4x - 4\)
Réduisons.
\(f’(x) = 3x^2 - 3\)
Nous trouvons bien le même résultat. Libre à vous de préférer l’une ou l’autre de ces deux techniques.
Corrigé 2
Ici aussi il est possible de d’abord développer la fonction avant de la dériver mais l’intérêt est moins évident. Aussi nous contenterons-nous d’appliquer directement la formule (ce qui n’est déjà pas si mal). Posons d’abord les éléments du calcul.
\(u(x) = \sqrt{x}\) donc \(u'(x) = \frac{1}{2\sqrt{x}}\)
\(v(x) = 2x - 5\) donc \(v'(x) = 2\)
Ensuite, dérivons.
\(g'(x) = \frac{2x - 5}{2\sqrt{x}} + 2\sqrt{x}\)
Il est toujours préférable de présenter l’expression d’une dérivée sous une forme factorisée.
\(g'(x) = \frac{2x - 5 + (2\sqrt{x})^2}{2\sqrt{x}}\)
\(\Leftrightarrow g'(x) = \frac{2x - 5 + 4x}{2\sqrt{x}}\)
\(\Leftrightarrow g'(x) = \frac{6x - 5}{2\sqrt{x}}\)
Pour déterminer \(g’(1),\) il suffit de remplacer \(x\) par 1. D’où \(g’(1) = 0,5.\)
Nombre dérivé avec une calculatrice TI-82 ou TI-83 : entrez l'expression de la fonction (touche en haut à gauche).
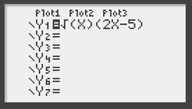
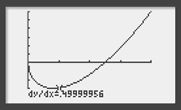
Pour que le nombre dérivé s’inscrive sur l’écran graphique, ajustez d’abord la fenêtre du graphe (le nombre dérivé doit se situer entre Xmin et Xmax). Ensuite, touches 2nd et Trace afin de se trouver sur le menu de calcul. Le nombre dérivé s'obtient avec le choix n°6. Validez. Le graphe apparaît. Comme nous cherchons \(g'(1),\) tapez 1 puis validez. Le résultat figure en bas. L’algorithme utilisé ne fournit pas toujours le résultat attendu et il convient peut-être d’arrondir celui-ci. En l’occurrence, si vous lisez 0,49999956, vous savez que vous pouvez traduire par 0,5, ce qui confirme bien le nombre dérivé tel que calculé « à la main ».
De nombreux autres exercices de dérivation de type « produit » existent sur ce site. Vous en débusquerez dans les pages exercices de dérivation de fonctions trigonométriques (exercice 1), fonction exponentielle au bac (exercice A1), fonction exponentielle, fonction logarithme au bac, etc.
