Principe de dérivation d'une fonction de degré 2
Cette page a été écrite pour les élèves des premières technologiques mais, bien sûr, elle peut aider quiconque n’a que moyennement compris un cours sur les dérivées…
Le principe
D’abord un petit topo sur la tangente à la courbe représentative d’une fonction en un point particulier : il s’agit d’une droite qui passe par ce point et qui « ressemble » le mieux possible à la courbe aux environs de ce point. Cette droite est la représentation d’une fonction affine, type de fonction déjà vu en seconde et même avant.
Supposons que notre point ait pour abscisse \(a.\) On appelle nombre dérivé de la fonction \(f\) en \(a,\) noté \(f’(a),\) le coefficient directeur de la tangente au point d’abscisse \(a.\)
Vite, un exemple...
Sur le graphe ci-dessous, réalisé avec le logiciel SineQuaNon, une fonction est représentée par la parabole rouge. Cherchons le nombre dérivé de cette fonction au point d’abscisse 1. Nous lisons \(f(1) = -2,5.\) Donc il faut tracer une droite qui ne frôle la courbe qu’au point de coordonnées \((1\,;-2,5).\) Cette droite est représentée en bleu (nous verrons comment plus loin car elle ne se trace pas « au pif »). Nous remarquons qu’elle ressemble bien à la courbe autour du point \((1\,;-2,5).\)
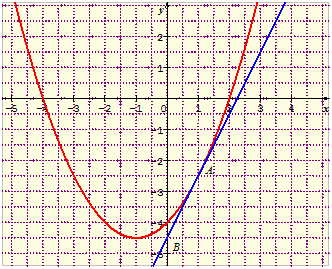
Par définition, la droite passe par le point \(A(1\,;-2,5).\) Mais elle passe aussi par le point \(B(0\,;-4,5).\) Espérons que vous n’avez jamais oublié cette chère formule du coefficient directeur \(a = \frac{y_B - y_A}{x_B - x_A}.\)
Donc, ici ça devient \(a = \frac{-4,5 + 2,5}{0 - 1} = 2\)
Ainsi, \(f’(1) = 2.\)
Cette technique est à utiliser lorsqu’on vous demande de trouver un nombre dérivé à partir d’une REPRÉSENTATION GRAPHIQUE. Mais il s'agit plus souvent de le déterminer à partir d’une EXPRESSION algébrique de type \(f(x) =…\)
Le plus simple consiste alors à dériver toute la fonction \(f\) pour en obtenir une autre \(f'.\) L’étape suivante consiste à remplacer \(x\) par la valeur de l’abscisse demandée dans l’énoncé.
Oui mais comment obtenir une dérivée ? Chaque type de fonction utilise une formule différente. Voyons celle de la fonction polynomiale du second degré.
Ce type de fonction a déjà été vu en classe de seconde : \(f(x) = ax^2 + bx + c\) (on appelle \(a\) le coefficient qui multiplie \(x^2,\) \(b\) le coefficient qui multiplie \(x\) et \(c\) est la constante). Une fonction du second degré est dérivable en tout point.
La dérivée s’écrit sous la forme \(f’(x) = 2ax + b.\) C'est donc une fonction affine, voire linéaire si \(b = 0.\)
Ainsi le carré est remplacé par une multiplication par 2, le \(x\) qui n’est pas au carré disparaît (ne subsiste que son coefficient) ainsi que la constante. Par exemple :
\(f(x) = 0,5x^2 + x – 4\) \(⇒ f’(x) = x + 1.\) Dans \(f'(x),\) \(x\) est multiplié par 1, obtenu par \(0,5 × 2.\)
Si l’on cherche le nombre dérivé de 1, il suffit de remplacer \(x\) par 1. Soit \(f’(1)\) \(= 1 + 1 = 2.\)
\(f\) est la fonction dont la courbe a été tracée ci-dessus. On trouve heureusement le même résultat qu’avec la lecture graphique...
Dernière chose, la détermination de l’équation de la tangente en un point d’abscisse \(a.\)
Il faut bien sûr connaître la formule : \(y = f(a) + f’(a)(x - a).\)
L’opération consiste donc d’une part à calculer \(f(a)\) et d'autre part à trouver l’expression de la dérivée puis de calculer \(f’(a).\)
Reprenons le même exemple.
Nous avons \(f(1) = -2,5\) et \(f’(1) = 2.\) L’équation de la tangente est donc \(y = -2,5 + 2(x - 1)\) soit \(y = 2x - 4,5.\)
Exercice
Soit une fonction \(f(x) = ax^2 + bx + c.\) On nous apprend que \(f(0) = 2,\) que l’équation de la tangente au point d’abscisse 1 est \(y = 7x,\) que l’équation de la tangente au point d’abscisse 2 est \(y = 11x - 6.\)
- Facile : trouver \(c\) puis calculer \(f’(1)\) et \(f’(2).\)
- Plus difficile : trouver \(a\) et \(b.\)

Éléments de correction
1 - Comme \(f(0) = 2,\) alors \((a × 0) + (b × 0) + c\) \(= 2,\) donc \(c = 2.\)
Les nombres dérivés sont les coefficients directeurs des tangentes. Donc \(f’(1) = 7\) et \(f’(2) = 11.\)
2- Pour trouver \(a\) et \(b,\) il faut poser un système de deux équations à deux inconnues (qui sont \(a\) et \(b\) et non pas \(x\) et \(y\)). On sait que \(f’(x) = 2ax + b.\)
Comme \(f’(1) = 7,\) alors \(2a + b = 7\) et comme \(f’(2) = 11\) alors \(4a + b = 11.\)
\(\left\{ {\begin{array}{*{20}{c}} {2a + b = 7}\\ {4a + b = 11} \end{array}} \right.\)
Employons la technique de la substitution.
\(\left\{ {\begin{array}{*{20}{c}} {b = 7 - 2a}\\ {4a + (7 - 2a) = 11} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {b = 7 - 2a}\\ {2a = 4} \end{array}} \right.\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a = 2}\\ {b = 3} \end{array}} \right.\)
Par conséquent \(f(x) = 2x^2 + 3x + 2\)
Voir l'exercice sur fonctions du second degré (extrait d'une épreuve du bac STMG).
Si vous êtes devenu un pro de la dérivation des fonctions du second degré, il est temps de passer à la vitesse supérieure et de se rendre en page de dérivation d'une fonction du troisième degré.
