Fonction logarithme et épidémiologie
Si vous êtes en terminale générale et que vous souhaitez vérifier votre dextérité à manier la fonction logarithme comme un virtuose des mathématiques, rien de tel qu’un extrait d’une épreuve de bac pour s’entraîner. Eh bien justement, un voici un. Il faisait partie du sujet du bac ES de juin 2014 en Asie.
Énoncé
- On étudie la propagation d’une maladie lors d’une épidémie.
Partie A
- Des relevés statistiques ont permis de modéliser, par une fonction \(f,\) le nombre de malades durant l’épidémie.
- Cette fonction est définie sur \([1\,; 26]\) par : \(f(t) = 24t \ln(t) - 3t^2 + 10\) où \(t\) est le nombre de semaines écoulées depuis le premier cas constaté et \(f(t)\) est le nombre de milliers de malades comptabilisés après \(t\) semaines.
- 1- On note \(f’\) la fonction dérivée de la fonction \(f.\)
- Montrer que pour tout réel \(t\) de l’intervalle \([1\,; 26],\) \(f’(t) = 24\ln(t) - 6t + 24.\)
- 2- Les variations de la fonction \(f’\) sont données dans le tableau suivant :
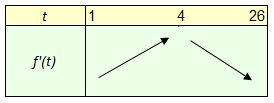
- a. Montrer que l’équation \(f’(t) = 0\) admet, dans l’intervalle \([1\,; 26],\) une solution et une seule qu’on notera \(\alpha\) et donner l’encadrement de \(\alpha\) par deux entiers naturels consécutifs.
- b. En déduire le signe de \(f(t)\) sur \([1\,; 26]\) et les variations de \(f\) sur \([1\,; 26].\)
- 3- Le réel \(f’(t)\) représente la vitesse de propagation de la maladie au bout de \(t\) semaines.
- a. Dans le contexte du problème, donner une interprétation de l’expression mathématique suivante : sur \([4\,; 26],\) \(f’\) est décroissante.
- b. À partir des questions précédentes, déterminer le nombre de semaines écoulées à partir duquel le nombre de malades par semaine a commencé à diminuer.
Partie B
- On admet que la fonction \(G\) définie par : \(G(t) = 12t^2 \ln(t) -6t^2\) est une primitive sur \([4\,; 26]\) de la fonction \(g\) définie par \(g(t) = 24t \ln(t).\)
- 1. Déterminer, sur \([4\,; 26],\) une primitive \(F\) de la fonction \(f.\)
- 2. On a trouvé que l’arrondi à l’entier \(\frac{1}{26 - 1} \times [F(26) - F(1)]\) est 202. Donner une interprétation de ce résultat dans le contexte du problème.
Correction
Partie A
1- Rappelons la formule de la dérivée d’un produit de fonctions \(u(t)v(t)\) : \(u’(t)v(t) + u(t)v’(t) .\) Ici, nous avons \(u(t) = 24t\) donc \(u’(t) = 24\) et \(v(t) = \ln(t)\) donc \(v’(t) = \frac{1}{t}.\)
\(f’(t) = 24\ln(t) + \frac{24t}{t} - 6t\)
Donc \(f’(t) = 24\ln(t) - 6t + 24\)
2- a. Selon le tableau de variation, la fonction \(f’\) est continue sur \([1\,;26].\)
Calculons \(f’(1) = 18,\) \(f’(4) \approx 33,3\) et \(f’(26) \approx -53,8\)
La fonction \(f’\) est strictement croissante et positive sur \([1\,;4].\) L’équation \(f’(t) = 0\) n’admet donc aucune solution sur cet intervalle.
La fonction \(f’\) est strictement décroissante et continue sur \([4\,; 26],\) \(f’(4) > 0\) et \(f’(26) < 0.\) Par conséquent, l’équation \(f’(t) = 0\) admet une solution et une seule sur cet intervalle.
Utilisons la calculatrice pour trouver l’encadrement de \(\alpha\) (techniques d’utilisation de la TI-82 en pages TVI et introduction à la continuité).
Il apparaît que \(\alpha\) est situé entre \(x = 14\) et \(x = 15.\)
b. La fonction \(f’\) étant positive sur \([1\,;\alpha],\) on en déduit que \(f\) est croissante sur cet intervalle ; \(f’\) étant négative sur \([\alpha\,;26],\) \(f\) est décroissante sur cet intervalle.
Quant au signe de \(f(t),\) le contexte nous indique qu’il est positif pour la bonne raison qu’il ne peut y avoir un nombre négatif de malades ! On peut éventuellement vérifier à la calculatrice que \(f(1) > 0\) et \(f(26) > 0\) (soit \(f(1) = 7\) et \(f(26) \approx 15\).)
3- a. Entre la quatrième et la vingt-sixième semaine, la vitesse de propagation de la maladie décroît (attention à ne pas écrire que c’est le nombre de malades qui décroît ! C’est le sens de variation de \(f\) qui donne cette information et non celui de \(f’,\) voir question suivante).
b. La valeur de \(t\) pour laquelle la fonction devient décroissante indique le moment où le nombre de malades commence à diminuer. Cette valeur est \(\alpha.\) On conclut que le nombre de malades commence à diminuer dans le courant de la quinzième semaine après le début de l’épidémie.
Partie B
1. \(f(t) = 24t \ln(t) - 3t^2 + 10\)
\(F(t) = 12t^2 \ln(t) - 6t^2 - t^3 + 10t + C\) (\(C\) étant un réel).
En ordonnant : \(F(t) = t^3 + (12 \ln(t) - 6)t^2 + 10t + C\)
2. La formule est celle de la valeur moyenne. Entre la première et la vingt-sixième semaine de l’épidémie, le nombre moyen de malades s’établit à 202 000.
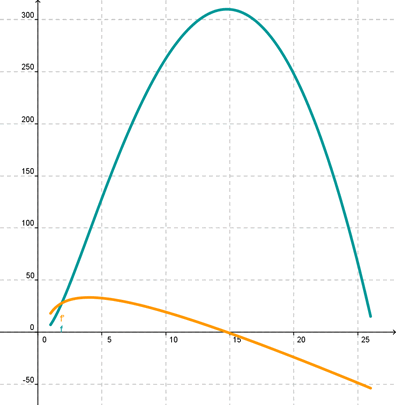
Pour information complémentaire, voici la courbe représentative de \(f\) (en bleu) et celle de \(f’\) (en orange). Réalisation sur GeoGebra.