Fonctions croissantes et décroissantes sur un intervalle
Encore une notion « basique » de maths à maîtriser dès la classe de seconde, juste après avoir revu quelques généralités sur les fonctions. Parfois expliquée de façon trop théorique, cette notion devient vite limpide grâce à l’arrivée salvatrice d’exemples…
Et ça tombe bien, cette page est justement rédigée pour les élèves de seconde.
Présentation
Une fonction est croissante sur un intervalle si pour tous les réels \(a \leqslant b\) de cet intervalle alors \(f(a) \leqslant f(b).\) La fonction conserve l’ordre. Voila pour l’explication théorique. Passons à un exemple simple.
Soit la fonction \(f:x \mapsto x + 1.\) Vous avez reconnu une fonction affine. Elle est croissante. Vérifions-le sur deux valeurs prises au hasard (1 et 2), d’abord par le calcul et ensuite graphiquement.
Soit \(a = 1\) et \(b = 2.\) On a bien \(a \leqslant b.\) On a aussi \(f(1) = 1 + 1 = 2\) et \(f(2) = 2 + 1 = 3.\) Donc \(f(a) \leqslant f(b).\)
Ci-dessous, la représentation de \(f\) figure en violet. L’intervalle se lit sur l’axe des abscisses (horizontal) et les valeurs de \(f\) sur l’axe des ordonnées. On voit bien que \(f(1) \geqslant f(2).\)
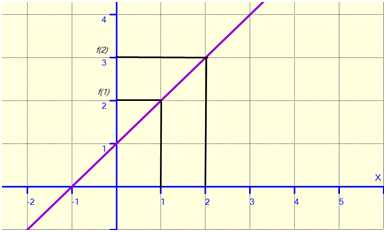
Si pour tous les réels \(a < b\) de l’intervalle (inégalité stricte), on a \(f(a) < f(b),\) la fonction est dite STRICTEMENT croissante. C’est d’ailleurs le cas dans cet exemple.
Une fonction est décroissante sur un intervalle si pour \(a \leqslant b\) de cet intervalle alors \(f(a) \geqslant f(b).\) La fonction change l’ordre. Prenons l’exemple de la fonction carré \(f: x \mapsto x^2\) sur \([-2\,; -1].\) Sur cet intervalle-ci, elle est décroissante. Ainsi, \(-2 < -1\) mais \(f(-2) > f(-1)\) puisque \(f(-2) = 2^2 = 4\) et \(f(-1) = 1^2 = 1.\) Illustration :
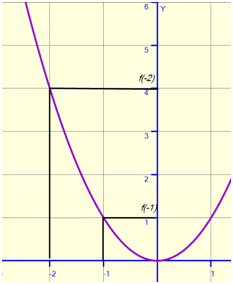
Enfin, une fonction est constante sur un intervalle si pour chaque réel \(a\) et \(b,\) \(f(a) = f(b).\) Graphiquement, une telle fonction se traduit par une droite horizontale. Mais ne rêvez pas, vous ne rencontrerez pas souvent des fonctions aussi simples au cours de vos études…
Lorsque sur un intervalle une fonction est toujours croissante, toujours décroissante ou toujours constante, on dit qu'elle est monotone sur cet intervalle.
Il est habituel que sur son ensemble de définition une fonction n’ait pas toujours le même sens de variation. C'est ce qui est illustré sur le graphe ci-dessus. On résume ces changements de cap dans un tableau de variation.
Si l’on ne dispose que de la courbe représentative d’une fonction mais pas de son expression algébrique, il est enfantin de déterminer son sens de variation : là où la courbe s’élève, la fonction est croissante, là où la courbe est orientée vers le bas, la fonction est décroissante.
Attention, un tableau de valeurs ne suffit pas pour déterminer un sens de variation car il peut très bien exister un retournement entre deux valeurs du tableau qui passe inaperçu !
Fonctions de référence
En classe de seconde, on étudie les fonctions linéaires et affines, carré et cube, ainsi que la fonction racine carrée et la fonction inverse.
La fonction linéaire ou affine est croissante si son coefficient directeur est positif, décroissante s’il est négatif et constante s’il est nul (la fonction est alors égale à un nombre et son expression ne comprend pas de \(x\).
La fonction carré est décroissante sur \(]-∞\,; 0]\) et croissante sur \([0 \,; +∞[.\) La courbe présentée plus haut montre d’ailleurs le retournement en 0. Les fonctions polynomiales de degré 2, de type \(f(x) = ax^2 + bx + c,\) sont croissantes puis décoissantes si \(a < 0\) et décroissantes puis croissantes si \(a > 0.\) Notez au passage que de telles fonctions peuvent être présentées comme le produit de deux fonctions affines. Ceci démontre que le produit de deux fonctions monotones sur un intervalle n'est pas toujours monotone (mais ceci dépasse le programme de seconde).
La fonction inverse est \(f:x \mapsto \frac{1}{x}.\) Elle est décroissante sur \(]-∞ \,; 0[\) et sur \(]0 \,; +∞[.\) D’accord, c’est un peu lourd de répéter qu’elle est décroissante sur les deux intervalles mais comme elle n’existe pas en 0, nous sommes obligés de présenter les choses ainsi.
Exemple
Démontrons que la fonction carré f est décroissante sur \(]-∞\,;0]\) et croissante sur \([0\,;+∞[.\)
Une telle démonstration ne doit pas utiliser de nombres car elle ne prouverait pas que le mécanisme fonctionne avec TOUS les réels. Reprenons donc nos deux réels quelconques \(a\) et \(b\) avec \(a \leqslant b.\)
Cas n° 1, \(a\) et \(b\) sont négatifs.
Il faut donc montrer que \(f(a) \geqslant f(b)\) c’est-à-dire que \(f(a) - f(b) \geqslant 0,\) donc \(a^2 - b^2 \geqslant 0\)
Rappelons l’identité remarquable \(a^2 - b^2\) \(=\) \((a + b)(a - b).\)
Or, \((a + b)\) est négatif puisque ces deux nombres sont négatifs et \((a - b)\) est négatif également puisque \(a\) est plus petit que \(b.\) Donc, \((a - b)^2 \geqslant 0\) puisque c’est le produit de deux nombres négatifs. La fonction est bien décroissante sur \(]-∞\,; 0].\)
Cas n° 2, \(a\) et \(b\) sont positifs.
Nous avons présenté le cas n° 1 de façon à faire comprendre la démonstration. Le cas n° 2 est démontré d’une façon plus formelle, telle que vous devriez la détailler si d'aventure on vous la demandait.
\(0 \leqslant a \leqslant b\)
\( \Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {a - b \leqslant 0}\\ {a + b \geqslant 0} \end{array}} \right.\)
\(\Leftrightarrow (a+b)(a-b) \leqslant 0\)
\(\Leftrightarrow a^2 - b^2 \leqslant 0\)
\(\Leftrightarrow f(a) - f(b) \leqslant 0\)
\(\Leftrightarrow f(a) \leqslant f(b)\)
\(f\) est croissante sur \([0\,;+\infty[.\)
