Cylindre de révolution
Depuis l’Antiquité, le cylindre est un solide indissociable de l’histoire de l’Humanité, tant pour des raisons esthétiques que techniques. Cette forme est celle des colonnes des temples égyptiens, grecs, romains, perses… mais on la trouve aussi dans les moteurs, les armes et les instruments de musique. Dans le règne végétal, elle est partout. Son étude en géométrie n’a donc rien d’abstrait, bien au contraire.

Présentation
Le cylindre désigne à la fois un solide et sa surface. Ce terme générique s’applique à des figures assez diverses mais nous ne nous intéresserons qu’au cylindre droit, ou cylindre de révolution, formé de deux disques reliés perpendiculairement sur tout leur diamètre. On l’appelle cylindre de révolution car on l’obtient aussi en faisant tourner un rectangle autour d’un axe.
Sa surface est donc constituée de trois parties : deux disques et une surface latérale.
Un cylindre de révolution est caractérisé par un rayon et une hauteur.
Historique
C’est Archimède qui, le premier, a déterminé la formule du volume d’un cylindre (ce dont il était particulièrement fier puisqu’il a demandé qu’elle soit inscrite sur sa tombe).
Archimède est né vers 287 av. J.-C. soit plus de deux siècles après la mort de Pythagore. Il a passé l’essentiel de sa vie à Syracuse, en Sicile. Il n’a pas été seulement un des plus grands mathématiciens de tous les temps ; il était aussi un physicien, un astronome et un ingénieur de génie (quoique le terme d’ingénieur est un peu anachronique). Nous ne savons pas grand chose de sa vie mais une bonne partie de ses écrits nous sont parvenus, par exemple sur l’approximation du nombre \(π.\)
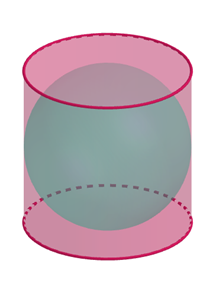
Qu’a-t-il déterminé ? Que le volume d'un cylindre est égal à 1,5 fois le volume de la boule qui y est inscrite. Cette proportion vaut aussi pour les surfaces.
Illustration avec GeoGebra :
Formules
Avec Archimède, nous avons vu le cas du cylindre dont la hauteur est égale à son diamètre. Mais c’est un cas particulier.
Le volume d’un cylindre de rayon \(r\) et de hauteur \(h\) est \(\mathscr{V} = π r^2h.\)
Pour calculer le volume d’un cylindre creux, par exemple un tuyau, il suffit de soustraire au volume calculé sur l’extérieur celui du cylindre interne constitué de vide.
Sa surface est égale aux aires des bases (\(2 × π r^2\)) plus l’aire latérale (\(2π rh\)). En factorisant, on peut exprimer sa surface ainsi : \(2 π r(r + h).\)
Patron
Le patron d’un cylindre droit est composé d’un rectangle et de deux disques qui lui sont contigus, sur des côtés opposés. Peu importe l’emplacement des disques le long des côtés du rectangle.

Attention, si les côtés contigus aux disques ne mesurent pas \(2 π r\) le patron est faux.
Équation cartésienne
Et en géométrie analytique ?
Dans un repère orthonormé \((O\, ;\overrightarrow{i}, ;\overrightarrow{j}, ;\overrightarrow{k})\) le cylindre de révolution d’axe \(Oz\) et de rayon \(r\) a pour équation \(x^2 + y^2 = r^2.\) On précise l’intervalle dans lequel se situe \(z\) si le cylindre n’a pas une hauteur infinie !

Exercice simple
Soit une boîte conique fermée. Son rayon est de 3 cm et sa hauteur de 20 cm.
Peut-on y ranger une baguette qui mesure 21 cm ?
Corrigé
Ce problème s’appuie sur le théorème de Pythagore dans l’espace. La baguette ne tiendra pas verticalement : sa taille limite est l’hypoténuse \(H\) d’un triangle rectangle dont les deux autres côtés sont la hauteur de la boîte et le diamètre de son fond.
Cherchons la taille maximale d’une baguette.
Le diamètre est égal à 6 et la hauteur à 20.
\(H^2 = 6^2 + 20^2 = 436\)
\(⇔ H = \sqrt{436} ≈ 20,88\)
Conclusion : la baguette est trop grande pour que l’on puisse refermer la boîte.
