Inéquation quotient (niveau seconde)
Sur cette page vous trouverez un exercice d’inéquation quotient, du niveau d’une classe de seconde (précisons qu’il cumule de nombreuses subtilités !). Le bref énoncé précède un corrigé très détaillé, prétexte à rappeler les aspects théoriques nécessaires. Que du bonheur.
Prérequis : vous devez absolument maîtriser les intervalles. Sinon, vous ne pourrez pas présenter les solutions. Ce serait dommage.
Exercice
Résoudre dans \(\mathbb{R} \backslash \{-2\}\) l’inéquation suivante :
\[\frac{x^2 + 4x - 1}{2x + 4} \geqslant 2\]
Commentaire
Il ne paie pas de mine, cet énoncé ; mais il va nous occuper un moment.
Résoudre une inéquation, c’est trouver toutes les valeurs de \(x\) qui vérifient l’inégalité. Vous comprenez déjà pourquoi celle-ci sera résolue dans l’ensemble des réels privé de la valeur -2. Elle conduirait à un dénominateur nul, ce qui est impossible. Ici, l’ensemble de définition est donné mais lorsque ce n’est pas le cas, il faut commencer par chercher les valeurs interdites.
Étape 1
Attention danger : ne pas faire de produit en croix pour écrire \(x^2 + 4x - 1 \geqslant 2(2x + 4)\) ! Le résultat serait faux. Il faut d’abord transposer tous les termes de l’inégalité du même côté puis les mettre au même dénominateur. La forme obtenue doit ensuite être factorisée pour que l’on puisse ultérieurement appliquer la règle des signes.
\(\frac{x^2 + 4x - 1}{2x + 4} - 2 \geqslant 0\)
\(\Leftrightarrow \frac{x^2 + 4x - 1}{2x + 4} - \frac{2(2x + 4)}{2x + 4} \geqslant 0\)
\(\Leftrightarrow \frac{x^2 + 4x - 1 - 4x - 8}{2x + 4} \geqslant 0\)
Vous avez remarqué que le dernier terme du numérateur est -8 et non +8. Il faut penser à distribuer le signe négatif !
Réduisons le numérateur.
\(\frac{x^2 - 9}{2x + 4} \geqslant 0\)
Avez-vous vu cette magnifique identité remarquable qui trône au numérateur ? Empressons-nous d’en donner la forme factorisée.
\(\frac{(x+3)(x-3)}{2x + 4} \geqslant 0\)
Et voilà. La première étape est terminée.

Étape 2
Il est clair que l’expression est nulle pour \(x = -3\) et pour \(x = 3.\) En effet, d’après le théorème du produit nul, notre numérateur s’annule si l’un de ses facteurs est nul.
L’étape 2 est donc celle de l’étude du signe de l’expression que nous avons obtenue. Le signe peut être positif ou négatif pour chacun des facteurs du numérateur ainsi que pour le dénominateur. Remarquons que dans chaque cas le coefficient de \(x\) est positif. Il s’ensuit que le signe de chacune des trois expressions est négatif pour les valeurs inférieures à celles qui les annulent et le signe est positif pour les valeurs supérieures. Un tableau de signes va nous permettre d’en faire la synthèse.
Celui-ci est réalisée avec le logiciel SineQuaNon. Un bouton permet d’accéder à la construction des tableaux de variations et des tableaux de signes.

Le tableau n’est pas construit par le logiciel à partir de l’expression d’une fonction. Il faut entièrement le définir avec du code. On clique sur le bouton Sgn pour réaliser un tableau de signes.
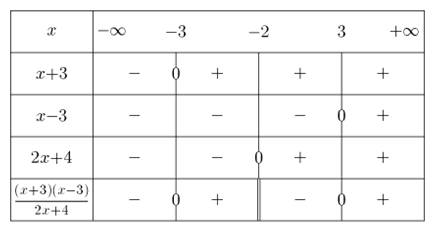
Pour information, le code permettant d’obtenir ce tableau :
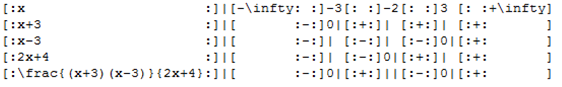
La dernière ligne du tableau, fondée sur la règle des signes, est celle qui nous permet de déterminer l’ensemble des solutions. La valeur interdite (-2 qui annule le dénominateur) est indiquée par une double barre.
Étape 3
La dernière étape consiste à déterminer l’intervalle pour lequel les valeurs de \(x\) vérifient l’inégalité. En l’occurrence, là où notre expression est positive ou nulle.
Rappelons que lorsque l’inégalité est au sens large comme ici, les crochets qui bornent l’intervalle des solutions sont fermés. Sauf bien sûr dans deux situations : sur l’infini et lorsque l’intervalle exclut une valeur. Ici, c’est -2 qui est une valeur interdite.
Par conséquent \(S = [-3\,; -2[ \;U \; [3\,; + \infty [.\)
Vérification
Il est pratique de vérifier graphiquement si aucune erreur de calcul s’est glissée…
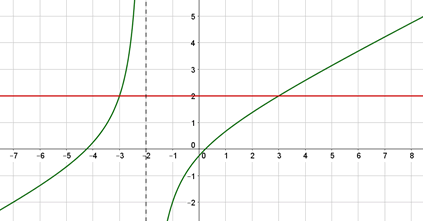
La courbe verte représente une fonction \(f\) définie par \(f(x) = \frac{x^2 + 4x - 1}{2x + 4}.\)
La droite rouge est située sur l’ordonnée 2.
Il suffit de voir pour quelles abscisses la courbe verte se situe au-dessus de la droite rouge (puisque le quotient doit être supérieur à 2). Malgré l'imprécision graphique, nous nous doutons bien que \(S\) \(=\) \([-3\,; -2[ \;U \; [3\,; + \infty [.\)
