Lissage de Winters sur schéma multiplicatif
Le lissage est une technique qui permet de prolonger une série chronologique afin d'établir une prévision à court terme. Il en existe de plusieurs types et le plus abouti est certainement le lissage de Winters sur schéma multiplicatif. La plupart des prévisions de ventes sont établies à partir de cette technique.
Rappels
Vous baignez certainement dans le lissage de Holt depuis votre tendre enfance : établissement d’une fonction localement linéaire dont la pente et le niveau sont estimés à partir de réalisations passées et de prévisions. Ces dernières sont déterminées à l’aide de deux paramètres, les constantes de lissage alpha et gamma. Celles-ci permettent de donner plus ou moins de poids aux dernières observations.
Si vous avez fait connaissance avec le lissage de Winters sur schéma additif, vous savez qu’un troisième paramètre est requis : un coefficient saisonnier delta.
Dès que l’on intègre une saisonnalité, on choisit un schéma de composition. Soit l’amplitude des mouvements saisonniers reste stable, soit elle varie avec la tendance. Si l'amplitude intersaisonnière est stable, le schéma est additif (on additionne à la tendance les mêmes variations saisonnières). Mais en général, ces variations périodiques sont d’autant plus marquées que les volumes sont importants, c’est-à-dire que le schéma de composition est multiplicatif.

Formule
\(\hat{y}_t(h)\) \(=\) \(s_{t+h}(a_th + b_t)\)
Exemple
Sur le même exemple que celui du cas additif, les prévisions deviennent ceci (tableau réalisé avec Excel, les tableurs étant parfaits pour traiter les relations de récurrence) :
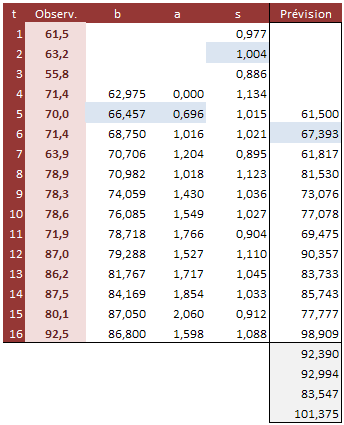
L’initialisation des valeurs \(a\) et \(b\) est la même que dans le cas additif. Le premier coefficient (0,977) est obtenu par \(\frac{61,5}{62,975}.\)
\(66,457\) \(=\) \(0,4 \times \frac{70}{0,977}\) \(+\) \((1 - 0,4) (62,975 + 0).\)
\(0,696\) \(=\) \(0,2 (66,457 - 62,975)\) \(+\) \(0 (1 - 0,2).\) Fidèle à elle-même, la même formule que dans le cas additif, également utilisée pour la méthode de Holt.
La valeur 1,004 est obtenue par \(\frac{63,2}{62,975}.\) L'année suivante, 1,015 sera obtenu par \(0,5 \times \frac{70}{66,457}\) \(+\) \(0,977 (1 - 0,5).\)
Enfin, \(67,393\) \(=\) \((66,457 + 0,696) × 1,004.\)
Les prévisions en grisées sont établies de façon très simple :
\(101,375\) \(=\) \([86,8 + (4 × 1,598)]\) \(×\) \(1,088\) aux arrondis près.
Le schéma multiplicatif complet
Pour terminer, mentionnons la possibilité d’un schéma multiplicatif complet, tout type de lissage pouvant bien sûr s’appliquer à une tendance exponentielle : \(\hat{y}_t(h)\) \(=\) \(s_{t+h} \times a_th \times b_t\)
Par transformation logarithmique, on retrouve le schéma additif.
