Loi à densité uniforme
Dans sa version à densité, la loi uniforme est la première loi de probabilité à être enseignée (en terminale pour la filière générale). Après l’indispensable définition, nous étudierons ses propriétés.
Note : cette page s’adresse principalement aux élèves de terminale générale (maths complémentaires) ainsi qu’aux étudiants. Pour les professionnels, voir plutôt la page sur la loi uniforme.
Définition
Soit un univers des possibles \(Ω,\) intervalle de \(\mathbb{R}\), et \(a\) et \(b\) deux réels tels que \(a < b.\)
On appelle loi uniforme sur \([a\,; b]\) la loi de probabilité dont la densité \(f\) est la fonction constante définie par :
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{{\rm{0\;si\;}}x < a}\\
{\frac{1}{{b - a}}{\rm{\;si\;}}a \leqslant x \leqslant b}\\
{{\rm{0\;si\;}}x > b}
\end{array}} \right.\]
Représentation :
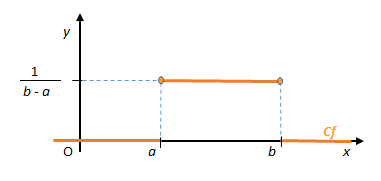
Fonction de répartition
La fonction de répartition \(F\) est définie par :
\[f(x) = \left\{ {\begin{array}{*{20}{c}}
{{\rm{0\;si\;}}x < a}\\
{\frac{x - a}{{b - a}}{\rm{\;si\;}}a \leqslant x \leqslant b}\\
{{\rm{0\;si\;}}x > b}
\end{array}} \right.\]
Représentation :
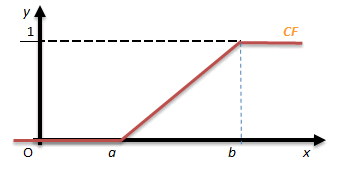
Espérance et variance
Soit \(X\) une variable aléatoire suivant une loi uniforme sur \([a\,;b]\) dont la fonction de densité est \(f.\) L'espérance d'une fonction de densité est définie par :
\[E(X) = \int_a^b {xf(x)dx} \]
Montrons que \(E(X)\) peut s’écrire de façon plus simple.
\[E(X) = \int\limits_a^b {x \times \frac{1}{{b - a}}} \]
Il n’est pas trop difficile de trouver une primitive…
\(E(X) = \left[ {\frac{{{x^2}}}{{2(b - a)}}} \right] = \frac{{{b^2} - {a^2}}}{{2(b - a)}}\)
Pour simplifier cette expression, détectons la belle identité remarquable du numérateur…
\(E(X) = \frac{(b + a)(b - a)}{2(b - a)} = \frac{a + b}{2}\)
C’est donc tout simplement la moyenne des deux bornes de l’intervalle…
La variance de \(X\) nous est donnée par \(V(X) = \frac{(b - a)^2}{2}\)
Calculs de probabilités
Soit \(X\) une variable aléatoire suivant une loi uniforme sur \([0\,;4].\)
Calculons \(P(X = 2),\) \(P(2 < X < 3)\) et \(E(X).\)
Comme la loi est continue, la probabilité d’obtenir une valeur précise est, par définition, nulle. Donc \(P(X = 2) = 0.\)
Nous allons déterminer \(P(2 < X < 3)\) de deux façons.
Premièrement par la densité : \(P(2 < X < 3) = \frac{1}{4}(3 - 2) = 0,25.\)
Deuxièmement par la fonction de répartition :
\(F(3) - F(2)\) \(=\) \(\frac{3-0}{4-0} - \frac{2-0}{4-0}\) \(=\) \(\frac{1}{4}\) \(=\) \(0,25\)
Notez que si les inégalités sont larges, le résultat est fort logiquement le même : \(P (2 \leqslant X \leqslant 3) = 0,25.\)
Enfin, l’espérance est très simple à calculer : \(E(X) = \frac{0+4}{2} = 2.\)
Le résultat est d’ailleurs assez intuitif…
Hasard
La loi uniforme modélise les tirages au hasard. Par exemple, si un logiciel choisit un nombre de façon aléatoire entre 0 et 1, la probabilité que celui-ci soit compris entre 0,3 et 0,5 est égale à \(0,5 - 0,3 = 0,2.\)
