Formule des probabilités totales
Une page pour décrire… une addition ! Reconnaissez que le niveau ne sera pas très élevé ! En effet, la formule des probabilités totales n’est pas le point le plus difficile du programme de maths de première générale. Mais elle est essentielle.
Partition de l’univers
Soit un univers \(Ω.\) Rappelons qu’en théorie des probabilités un univers est l’ensemble des évènements possibles.
Une partition de \(Ω\), ou système complet d’évènements, est constitué de sous-ensembles de \(Ω\) disjoints, non nuls et dont la réunion recouvre \(Ω.\)
Soit par exemple \(Ω = \{1\, ;2\, ;3\, ;4\, ;5\, ;6\}.\) C’est le résultat d’un lancer de dé. Si \(P\) est l’évènement « le numéro tiré est pair » et \(I\) est « le numéro tiré est impair » alors \(P\) et \(I\) forment une partition de l’univers. Soit \(S\) l’évènement « le numéro tiré est 6 ». Alors \(P\) et \(S\) ne forment pas une partition de l’univers. D’abord parce que 6 est compris deux fois, ensuite parce que les nombres impairs sont oubliés.
Par définition, un évènement et son complémentaire forment une partition. Soit \(\overline S \) l’évènement « le nombre tiré est différent de 6 ». On a bien \(Ω = S ∪ \overline S .\)
Et voici la formule…
Soit \(n\) un entier naturel non nul et \({A_1, A_2,…,A_n}\) une partition de \(Ω\) et soit \(B\) un évènement.
\(P(B)\) \(= P({A_1} \cap B) + P({A_2} \cap B) + ... + P({A_n} \cap B)\)
Arbres de probabilités
Rappelons quelques principes des arbres pondérés. Il s’agit de graphes dont les nœuds représentent les évènements et les branches les liens entre deux évènements. Une branche est affectée d’une probabilité.
Prenons un exemple, ce sera plus clair.
Soit un ensemble d’appartements F2 et F3. Certains sont habités par leur propriétaire, d’autres par des locataires. On sait qu’il y a \(40\%\) de F2 et, parmi ceux-ci, \(80\%\) sont loués. On sait aussi que \(30\%\) des F3 sont habités par leurs propriétaires.
Un enquêteur frappe à la porte d’un appartement. Il élabore des probabilités…
Les évènements F2 et F3 forment une partition de l’univers puisqu’il n’existe pas d’autre type d’appartement et qu’un appartement ne peut être à la fois F2 et F3. Donc si la probabilité que l’appartement soit un F2 est de 0,4 c’est que la probabilité qu’il soit un F3 s’établit à \(1 - 0,4 = 0,6.\)
Même raisonnement pour le critère propriétaire (\(P\)) ou locataire (\(L\)).
Ceci nous conduit à un arbre pondéré qui ressemble à ceci (réalisation avec le logiciel Sine qua non) :
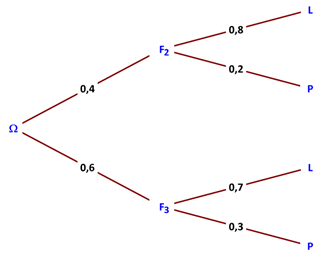
En toute logique, la somme des probabilités partant d’un même évènement est toujours égale à 1.
Quelle est la probabilité qu’un appartement soit loué et que ce soit un F2 ? \(P(F2 ∩ L) = 0,4 × 0,8 = 0,32.\)
La probabilité 0,8 qui apparaît en haut du graphe est une probabilité conditionnelle. \(P_{F2}(L) = 0,8.\)
Et les probabilités totales dans tout ça ?
Si l’on cherche la probabilité qu’un locataire occupe l’appartement, celle-ci n’apparaît pas directement sur l’arbre puisque deux branches sont concernées (F2 et F3 qui forment une partition de l’univers). Il faut donc additionner les probabilités d’être locataire dans un F2 et d’être locataire dans un F3.
\(P(L)\) \(= P(L ∩ F2) + P(L ∩ F3)\) \(= P(F2) × P_{F2}(L) + P(F3) × P_{F3}(L)\) \(= 0,4 × 0,8 + 0,6 × 0,7\) \(= 0,74.\)
Exercice
Cet exercice est extrait de l’épreuve de maths du bac ES, septembre 2019, Antilles-Guyane.
- Un grossiste en flacons de parfum souhaite étudier la qualité des flacons qu’il reçoit.
Il a reçu 1 500 flacons d’un certain modèle provenant de deux sites de production différents, le site A et le site B. Sur les 1 500 flacons de ce modèle reçus, 900 proviennent du site A, les autres du site B.
Le grossiste s’intéresse à l’aspect du flacon. Parmi les flacons provenant du site A, \(95\%\) ont un aspect conforme au cahier des charges tandis que \(92\%\) des flacons provenant du site B ont un aspect conforme.
Il prélève au hasard un des flacons qu’il a reçus lors de la dernière livraison.
On note :
\(A\) l’évènement « le flacon provient du site A » ;
\(B\) l’évènement « le flacon provient du site B » ;
\(C\) l’évènement « le flacon a un aspect conforme au cahier des charges ».
1- Déterminer la probabilité que le flacon provienne du site A et ait un aspect conforme au cahier des charges.
2- Montrer que la probabilité que le flacon ait un aspect conforme au cahier des charges est 0,938.

Corrigé
1- Nous cherchons la probabilité de l’évènement \(A ∩ C.\)
La probabilité que le flacon provienne du site A s’établit à \(\frac{900}{1500},\) soit 0,6.
\(P(A ∩ C) = P(A) × P_A(C)\) \(=0,6 × 0,95\) \(= 0,57.\)
2- Nous cherchons \(P(C).\)
Les évènements \(A\) et \(B\) forment une partition de l’univers. Donc, d’après la formule des probabilités totales :
\(P(C) = P(A ∩ C) + P(B ∩ C)\)
\(P(A ∩ C)\) a été calculée à la question précédente. Refaisons la même opération pour \(P(B ∩ C).\)
\(P(C) = 0,57 + 0,4 × 0,92\) \(= 0,938.\)
La probabilité que le flacon soit conforme s’établit à 0,938.
