Loi et utilisations du khi-deux
Voici une loi de probabilité bien pratique. La courbe du \(\chi^2\) n’est pas employée comme reflet de la distribution d'un caractère statistique bien que son géniteur, Karl Pearson, cherchait à rendre compte de distributions asymétriques de phénomènes observés, mais bien dans le cadre des probabilités.
D’abord nous verrons qui peut suivre une distribution du \(\chi^2\) car cet exploit n’est pas donné à tout le monde. Ensuite, cette loi fera une entrée triomphale sous forme de graphe puis elle nous présentera ce dont elle est capable.
Fiche signalétique
C’est la loi que suit une somme de variables aléatoires (v.a) gaussiennes indépendantes, centrées, réduites et mises au carré. Bien entendu, cette somme est elle-même une v.a.
Si l’on observe \(n\) v.a, la distribution suit une loi du \(\chi^2\) à \(n\) degrés de liberté (ddl). De fait, il existe autant de distributions du \(\chi^2\) que de valeurs de \(n.\) Deux précisons : on analyse des effectifs et non des pourcentages ou des probabilités, et au-delà d’une trentaine, l’approximation par la loi normale est possible.
Dès lors qu’il existe des liaisons entre v.a, le nombre de ddl est [\(n\) \(-\) nombre de liaisons].
Exemple :
![]()
D’abord, on voit que ce tableau montre un effectif de 2 en modalité \(A.\) Or, une classe doit contenir au moins cinq valeurs pour être « khideusable ». Si l’on regroupe \(A\) et \(B,\) on obtient un tableau de quatre cases, mais il existe une liaison entre elles : il suffit de connaître les quatre premières pour en déduire la dernière car le total est un élément connu a priori. Par conséquent, on retient trois ddl.
Autre exemple. Soit le tableau de contingence suivant (chaque case contient un effectif), dont l'établissement a été possible grâce à la connaissance des effectifs marginaux :
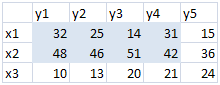
Les liaisons s’effectuent en colonnes et en lignes. Seules huit cases ne peuvent être devinées (nous avons arbitrairement surligné celles qui se trouvent en haut à gauche ; il faut se souvenir que l’on « évacue » une ligne et une colonne). Nombre de ddl \(=\) \(8.\)

Revenons à la théorie.
La formule de la densité de probabilité, qui inclut la fonction gamma, a fière allure :
\(g_n(x)\) \(=\) \(\displaystyle{\frac{1}{\Gamma \left( \frac{n}{2} \right) 2^{\frac{n}{2}}} x^{\frac{n}{2}-1}e^{-\frac{x}{2}}}\) avec \(x \geqslant 0.\)
Ajoutons à ceci la propriété d’additivité de cette loi, que l’on devine d’ailleurs au vu de ce que nous vous avons raconté auparavant. Si \(X\) et \(Y\) sont des v.a indépendantes qui suivent des lois du \(\chi^2\) à respectivement \(n\) et \(m\) ddl, alors \(X + Y\) suit tout simplement une loi du \(\chi^2\) à \(n + m\) ddl.
L’espérance mathématique est égale au nombre de ddl \(n\) (vérifiez-le pifométriquement sur les courbes ci-dessous) et la variance est égale à \(2n\) (on constate aussi que l’étalement des densités de probabilité est lié au nombre de ddl).
Album photos
La fonction de densité diffère selon le nombre de ddl. Commençons par les degrés 1 et 2 qui sont des cas particuliers (réalisations sur Gretl) :
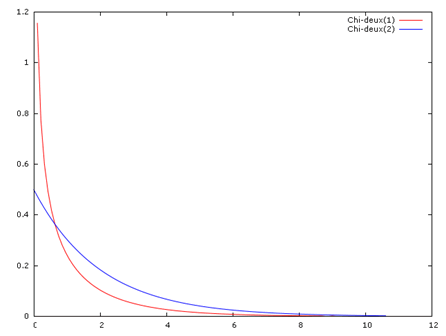
Ensuite, les courbes ressemblent de plus en plus à celle de la loi normale au fur et à mesure que le nombre de ddl augmente, en application du théorème central-limite (représentation de trois en trois ci-dessous, jusqu’à trente ddl).
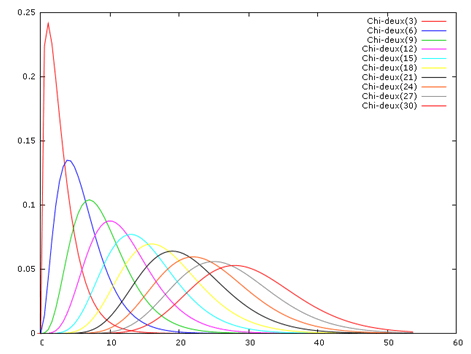
Les grands exploits du khi²
La distribution du \(\chi^2\) est utilisée pour les tests d’indépendance. Sur la page consacrée à cette ludique activité (mais si, mais si), j’ai pris l’exemple d’un \(\chi^2\) à douze ddl (donc courbe rose ci-dessus) avec une valeur de 27,2. On constate que les chances de tomber sur cette valeur sont minces. En page sorties de logiciel pour test du \(\chi^2\), l’exemple présente cette fois-ci trois ddl (première courbe rouge ci-dessus) et un \(\chi^2\) de 40. Il est évident que les chances sont cette fois-ci quasi nulles pour qu’une valeur de 40 soit prise par cette courbe.
Les arbres de décision CHIAD intègrent ces tests d’indépendance.
En second lieu, cette loi permet de tester la qualité d’ajustement entre une distribution observée et une distribution théorique (voire entre deux distributions observées). Historiquement, ce fut d'ailleurs sa première utilisation, découverte par Karl Pearson en 1900.
En revanche, l’expression « distance du \(\chi^2\) », utilisée notamment dans le champ de l’AFC, signifie que la métrique est la même que celle utilisée par les tests du \(\chi^2\) pour évaluer les distances entre unités statistiques, variables ou modalités, mais la loi stricto sensu n’intervient pas.
Enfin, par sa définition même, la variance d’un échantillon de taille \(n\) est une v.a qui suit une loi du \(\chi^2\) à \(n - 1\) ddl.
Pour mémoire, le rapport de deux v.a indépendantes suivant chacune une loi du \(\chi^2,\) divisées par leurs nombres respectifs de ddl, suit quant à lui une loi de Fisher (dont l'utilité apparaît en page test du F).
