Suites périodiques, suites sans limite
C’est en classe de terminale générale que l’on travaille sur les limites de suites. Or, toutes les suites n’ont pas de limite. Cette page n’a pas d’autre prétention que d’en montrer quelques exemples à titre de complément. En effet, elles ne figurent pas expressément au programme mais il est possible de les rencontrer au détour d’un exercice.
Les illustrations de cette page ont été réalisées en ligne avec WIMS.
https://wims.univ-cotedazur.fr/wims/
Suites périodiques
Soit \(p ∈ \mathbb{N}.\) Une suite est de période \(p\) si, pour tout entier naturel \(n,\) \(u_{n + p} = u_n.\)
Les plus célèbres sont les suites géométriques de raison -1. Elles sont de période 2, quel que soit le premier terme (non nul).
Par exemple si \(u_0 = 2\) alors \(u_1 = 2 × (-1) = -2,\) \(u_2 = 2 × 1 = 2,\) etc. (2 pour chaque valeur paire de \(n\) et -2 pour chaque valeur impaire).
Une suite stationnaire est périodique, de période 1.
Une suite périodique est toujours bornée et jamais strictement monotone (ce qui paraît évident).

Exemple
Calculons les premiers termes de la suite \((u_n)\) définie par \(u_0 = 0\) et \(u_{n + 1} = -u_n + 10\) pour tout \(n\) appartenant à \(\mathbb{N}\) puis montrons qu’elle est périodique.
\(u_0 = 0,\) \(u_1 = 10,\) \(u_2 = 0,\) \(u_3 = 10,\) \(u_4 = 0,\) \(u_5 = 10,\) \(u_6 = 0\) (bon, ça suffit comme ça).
Nous pouvons conjecturer que la période est 2. Démontrons-le.
\(u_{n + 2} =-u_{n + 1} + 10\) \(= -(-u_n + 10) + 10\) \(= u_n - 10 + 10 \) \(= u_n\)
Suites non périodiques
Une suite peut prendre des valeurs de plus en plus éloignées de zéro mais parfois positives et parfois négatives. Il n’y a donc aucune limite. Soit par exemple une suite de type \(u_n = a^n\) avec \(a < -1\) : lorsque \(n\) est pair les termes sont positifs et lorsque \(n\) est impair ils sont négatifs, tout en s’éloignant de zéro.
Illustration avec la représentation de \((u_n)\) définie par \(u_n = (-1,1)^n\) qui est une suite géométrique de raison strictement inférieure à -1.
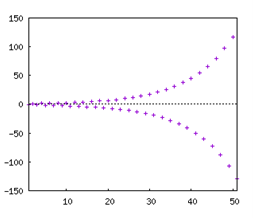
D’autres suites de ce type sont des composées de suites périodiques qui dépendent aussi de \(n.\)
Prenons par exemple la suite périodique \((u_n)\) définie par \(u_n = \cos (nπ).\) Nous avons la suite \((v_n)\) définie par \(v_n = -n \cos (nπ)\) qui entre dans cette catégorie.
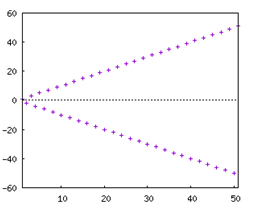
Exercice
Soit la suite \((u_n)\) définie par \(u_0 = 2\) et par \(u_{n+1}\) \(=\) \(\displaystyle{\frac{u_n - 2}{2u_n - 1}}\)
Montrer qu'elle est de période 2.
Corrigé
Pour montrer qu’une suite est de période 2, il faut arriver à \(u_{n+2} = u_n.\) Ceci consiste à transformer l’écriture de \(u_{n+2}.\)
\(\displaystyle{u_{n+2} = \frac{u_{n+1} - 2 }{2u_{n+1} - 1 }}\)
Remplaçons \(u_{n+1}\) par son expression en \(u_n.\)
\(u_{n+2}\) \(=\) \(\displaystyle{\frac{\frac{u_n - 2 }{2u_n - 1} - 2}{2 × \frac{u_n - 2}{2u_n - 1} - 1}}\)
\(⇔ u_{n+2}\) \(=\) \(\displaystyle{\frac{\frac{u_n - 2 - 2(2u_n - 1)}{2u_n - 1}}{\frac{2u_n - 4 - (2u_n - 1)}{2un - 1}}}\)
\(⇔ u_{n+2}\) \(=\) \(\displaystyle{\frac{u_n - 2 - 4u_n + 2}{2u_n - 4 - 2u_n + 1}}\)
\(⇔ u_{n+2}\) \(=\) \(\displaystyle{\frac{-3u_n}{-3} = u_n}\)
Comme \(u_n = u_{n+2}\) la suite \((u_n)\) est de périodicité 2.
Notez que cette technique devient vite lourde lorsque la périodicité est supérieure à 2. Rappelons que vous lisez une page d’information pour élèves de terminale et non un mode d'emploi permettant de se dépêtrer de toutes les situations.
