Suites majorées, minorées et bornées
Alors que certaines suites, libres comme l’air, vont batifoler dans les territoires infinis, d’autres se restreignent à un cadre rigide. Elles sont bornées. Intéressons-nous à elles, ça les consolera.
Définitions
Soit deux réels \(m\) et \(M\) tels que \(M \geqslant m.\) Soit \(n\) un entier naturel, éventuellement infini.
Une suite \((u_n)\) est majorée par \(M\) si, pour tout \(n,\) \(u_n \leqslant M.\)
Si par exemple 2 est la plus grande valeur prise par une suite, 2 est un majorant. Mais 3 aussi en est un. Toute suite majorée admet une infinité de majorants.
\((u_n)\) est minorée par \(m\) si, pour tout \(n,\) \(u_n \geqslant m.\) Toute suite minorée admet une infinité de minorants.
\((u_n)\) est bornée si pour tout \(n,\) \(m \leqslant u_n \leqslant M.\)
Une suite bornée est donc minorée et majorée.
Démonstration
On démontre qu’une suite est bornée grâce à la récurrence, aux opérations sur les limites, ou tout simplement en utilisant ses connaissances des fonctions usuelles.
Par exemple, considérons la suite \((u_n)\) définie par \(u_n = \sin(n).\) On sait qu’un sinus est compris entre -1 et 1. Nous en déduisons que \(u_n\) est borné par -1 et 1.
Limites
Une suite peut avoir ou non une limite. Si celle-ci existe, elle est soit finie soit infinie (si elle n'existe pas, vous en saurez plus en page de suites sans limite).
Lorsqu'en terminale on en découvre les définitions, elles peuvent sembler un peu bizarres. Pourtant, elles doivent paraître naturelles pour qui se destine à approfondir certaines branches des maths au cours d'études supérieures.
La suite \((u_n)\) admet pour limite le réel \(m\) si, à partir d'un certain rang, toutes les valeurs \(u_n\) appartiennent à un intervalle ouvert contenant \(m.\)
Elle admet pour limite \(+ \infty\) si tout intervalle \(]m\,; +\infty[\) contient toutes les valeurs \(u_n\) à partir d'un certain rang.
Exercice 1
Soit la suite \((u_n)\) définie sur \(\mathbb{N}\) par \(u_0 = 1\) et \(u_{n+1} = 0,5u_n - 1.\) Montrer qu’elle est minorée par -2 et majorée par 1.
Exercice 2
Démontrer que la suite \((v_n)\) définie sur \(\mathbb{N}^*\) par \(v_n = \sqrt{n^2 - 1} - n\) est bornée.
Corrigé 1
Comme nous sommes en présence d’une suite de type \(u_{n+1} = f(u_n),\) la démonstration par récurrence s’impose.
Proposition. \(P(n) : -2 \leqslant u_n \leqslant 1.\)
Initialisation. \(u_0 = 1,\) donc \(-2 \leqslant u_0 \leqslant 1.\) \(P(0)\) est vraie.
Hérédité. Supposons que l'encadrement de \(P(n)\) est vrai pour un entier \(n.\)
Alors, \(-2 \leqslant u_n \leqslant 1\)
Donc, \(-1 \leqslant 0,5u_n \leqslant 0,5.\)
Il s’ensuit que \(-2 \leqslant 0,5u_n - 1 \leqslant -0,5.\)
Selon l’énoncé, \(0,5u_n - 1\) n’est autre que \(u_{n+1},\) donc \(-2 \leqslant u_{n+1} \leqslant -0,5.\)
Donc \(P(n)\) est vraie pour tout entier \(n.\)
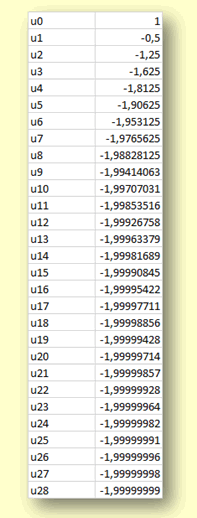
Une rapide vérification avec Excel permet de confirmer qu’à partir de \(u_1,\) -0,5 est un majorant :
Corrigé 2
Nous devons cette fois-ci étudier une suite de type \(v_n = f(n).\) Il faut transformer son expression car en l’état, il n’est pas possible de borner \((v_n).\)
L’idée est de multiplier l’expression par sa quantité conjuguée, ce qui aura pour double effet d’introduire un dénominateur et de supprimer toute variable au numérateur.
\(v_n\) \(=\) \(\displaystyle{\frac{(\sqrt{n^2 - 1} - n)(\sqrt{n^2 - 1} + n)}{\sqrt{n^2 - 1} + n}}\)
\(v_n\) \(=\) \(\displaystyle{\frac{n^2 - 1 - n^2}{\sqrt{n^2 - 1} + n}}\) \(=\) \(\displaystyle{\frac{-1}{\sqrt{n^2 - 1} + n}}\)
On constate aisément que \(-1 \leqslant v_n < 0.\)

