Exercices de dérivation de fonctions puissance
Sur cette page nous vous proposons quelques exercices de dérivées de fonctions composées de forme \((u(x))^n\) (\(n\) étant un entier relatif). Le niveau de difficulté correspond à ce que l’on peut attendre d’un élève de terminale générale.
Avant de commencer…
Considérons \(u(x)\), expression d'une fonction \(u\) définie et dérivable sur un intervalle \(I.\)
Considérons aussi une fonction \(f\) d'expression un peu plus compliquée, définie par \(f(x) = (u(x))^n,\) \(n\) étant un entier relatif non nul. Quid de sa dérivée sur \(I\) ?
\(f'(x) = n \times u'(x) \times (u(x))^{n-1}\)
Attention, \(u(x)\) ne doit pas être nulle si \(n < 0.\) Si cela ne vous semble pas évident, souvenez-vous que \(u^{-n} = \frac{1}{u^n}\)
Échauffement
Dérivons la fonction suivante, définie sur \(\mathbb{R}\) : \(g:x \mapsto {\left( {{x^2} + 4} \right)^3}\)
Ce qu’il faut trouver :
\(g’(x) = 3 \times (2x) \times (x^2 + 4)^2\)
\(g’(x) = 6x(x^2 + 4)^2\)
Exercice 1
Dériver la fonction suivante, définie sur \(\mathbb{R} \backslash \{0,5\}\)
\(h : x \mapsto \left(\frac{1}{2x - 1}\right)^2\)

Exercice 2
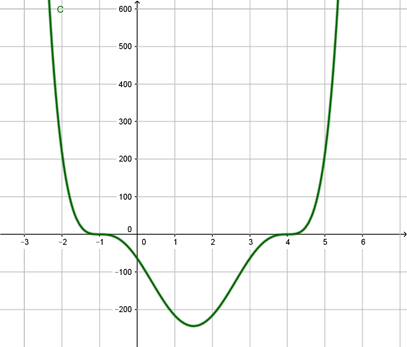
Soit la fonction \(f\) définie sur \(\mathbb{R}\) par \(f(x) = (x^2 - 3x - 4)^3\) et \(\mathscr{C}\) sa courbe représentative. Calculer son nombre dérivé en -1 et tracer \(\mathscr{C}.\)
Exercice 3
Soit la fonction \(u,\) définie sur \(\mathbb{R} \backslash \{-1\}\).
\(u(x) = \left(\frac{2x}{x + 1}\right)^4\)
Quelle est sa dérivée ?
Corrigé 1
Rappelons comment dériver cette forme de fonction :
\(\left(\frac{1}{u(x)}\right)' = -\frac{u'(x)}{(u(x))^2}\)
Il s’ensuit que la dérivée de \(\frac{1}{2x - 1}\) est \(-\frac{2}{(2x - 1)^2}.\)
Ainsi…
\(h'(x)\) \(= -\frac{2 \times 2}{(2x-1)^2} \times \frac{1}{2x - 1}\)
\(\Leftrightarrow h'(x) = -\frac{4}{(2x - 1)^3}\)
Corrigé 2
Cette fonction n’est pas très retorse.
\(f’(x) = 3(2x - 3)(x^2 - 3x - 4)^2\)
\(f’(-1) = 3 × (-5) × 0 = 0\)
Corrigé 3
Considérons la fonction \(v\) définie par \(v(x)\) telle que \(v(x)^4 = u(x).\)
Déterminons sa dérivée \(v’(x)\) (voir la page dérivée d’une fonction quotient si le souvenir de la formule est trop lointain).
\(v'(x)\) \(=\frac{2(x + 1) - 2x}{(x + 1)^2}\) \(= \frac{2}{(x + 1)^2}\)
Par conséquent :
\(u'(x) = 4 \times \frac{2}{(x + 1)^2} \times \left(\frac{2x}{x + 1}\right)^3\)
\(\Leftrightarrow u'(x) = \frac{8}{(x + 1)^2} \times \frac{8x^3}{(x + 1)^3}\)
\(\Leftrightarrow u'(x) = \frac{64x^3}{(x + 1)^5}\)
