Positions et encadrements de courbes
Sur cette page vous trouverez deux exercices corrigés dont l’objet est de déterminer les positions relatives de courbes représentatives de fonctions. Le niveau de difficulté est celui d’une première générale.
Exercice 1
Soit les fonctions \(f\) et \(g\) définies sur \([0\,;+∞[\) par \(f(x) = 4 \sqrt{x}\) et \(g(x) = 4x+1.\)
Étudier les positions relatives de leurs courbes représentatives.

Exercice 2
Soit les fonctions \(f,\) \(g\) et \(h\) définies sur \([0\,;+∞[\) par :
- \(f(x) = 1 - x - x^2\)
- \(g(x) = 1 - x\)
- \(h(x) = \frac{1}{1+x}\)
Soit \({\mathscr{C}_f,}\) \({\mathscr{C}_g}\) et \({\mathscr{C}_h}\) leurs courbes représentatives.
Comparer \(g\) et \(f\) puis \(g\) et \(h\) ainsi que les positions respectives de leurs courbes. Conclure.
Corrigé 1
Pour déterminer par le calcul quelle est la courbe qui est au-dessus de l’autre et sur quel intervalle, il faut étudier le signe d’une fonction qui est la différence entre \(f\) et \(g.\)
Soit \(h = g - f\)
\(h(x) = 4x + 1 - 4\sqrt{x}\)
Cela n’a pas dû échapper à votre coup d’œil, il s’agit d’une identité remarquable ! En effet, \(h(x) = (2\sqrt{x} - 1)^2.\)
Comme un carré est toujours positif ou nul, \(h\) est positive. Donc \(g - f \geqslant 0\) ce qui équivaut à \(g \geqslant f.\) Il s’ensuit que la courbe représentant \(g\) est au-dessus de celle qui représente \(f.\) Mais elles peuvent aussi être confondues en un ou plusieurs points, c’est-à-dire là où \(h\) est nulle. Vérifions-le.
\((2\sqrt{x} - 1)^2 = 0\)
\(\Leftrightarrow 2\sqrt{x} - 1 = 0\)
\(\Leftrightarrow 2\sqrt{x} = 1\)
\(\Leftrightarrow \sqrt{x} = \frac{1}{2}\)
\(\Leftrightarrow x = - \frac{1}{4}\) ou \(x = \frac{1}{4}\)
L'équation admet deux solutions mais comme nos fonctions \(f\) et \(g\) ne sont définies que pour les valeurs positives, leurs courbes représentatives ne sont confondues qu’au point d’abscisse \(\frac{1}{4}.\)
Ci-dessous, un repère dont les abscisses sont limitées à l'intervalle \([0\,;1]\) permet d'obtenir le graphe suivant avec la calculatrice TI-82 :
Corrigé 2
Voici un exercice assez classique d’encadrement.
Étudions d’abord \(g - f.\)
\(g(x) - f(x) = 1 - x - 1 + x + x^2\)
\(\Leftrightarrow g(x) - f(x) = x^2\)
Là aussi, nous obtenons un carré. Par conséquent \({\mathscr{C}_g}\) se situe au-dessus de \({\mathscr{C}_f},\) sauf au point d’abscisse 0 où ces courbes sont confondues. D’ailleurs, \(f(0) = g(0) = 1.\)
Étudions \(h - g.\)
\(h(x) - g(x) = \frac{1}{1 + x} - (1 - x)\)
\(\Leftrightarrow h(x) - g(x) = \frac{1}{1 + x} - \frac{(1 - x)(1 + x)}{1 + x}\)
\(\Leftrightarrow h(x) - g(x) = \frac{1}{1 + x} - \frac{1 - x^2}{1 + x}\)
\(\Leftrightarrow h(x) - g(x) = \frac{x^2}{1 + x}\)
Là encore, nous obtenons un résultat positif sur l’ensemble de définition, sauf en 0 où les fonctions ont la même valeur. Donc, \(h \geqslant g.\)
Il s’ensuit que, hormis en 0, \(h > g > f.\) On dit que la fonction affine \(g\) est encadrée par \(h\) et par \(f.\)
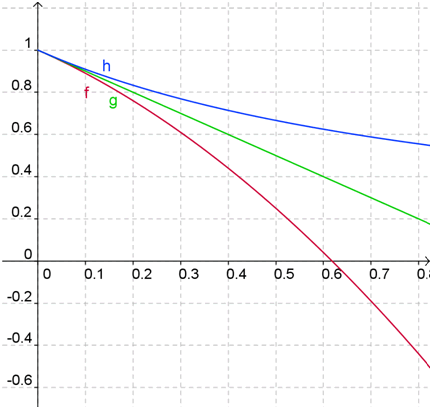
Ci-dessous, les trois courbes ont été tracées avec Geogebra.
Rappel du tracé de courbe limité à un intervalle : par exemple, pour tracer \({\mathscr{C}_g}\) entre 0 et 1, il faut entrer dans le champ de saisie Fonction[g(x)=1-x,0,1].