Acceptation de la rupture de stock en univers certain
La gestion des stocks s’appuie sur un ensemble de techniques visant toute une optimisation, un juste équilibre entre les coûts liés au stockage et un service dû aux « clients » (consommateurs, ligne de montage, etc.). Il existe toujours une technique mieux adaptée que les autres en fonction du contexte. Des contraintes sont liées au produit, au marché, aux impératifs de production... L’une d’entre elles est dite « de Wilson avec pénurie ». De quoi s’agit-il ?
Amélioration du modèle de Wilson
Le modèle de Wilson est la technique « basique » de la gestion de stocks. Très théorique, il est complété de diverses améliorations qui lui permettent de mieux coller à la réalité, parmi lesquelles la prise en compte de tarifs dégressifs ou encore l’acceptation d’une rupture de stocks.
N’assimilons pas la survenance d’une pénurie avec la conséquence d’un modèle aléatoire mal ficelé. On se situe ici dans le cadre d’un avenir certain et la rupture est parfaitement assumée. Simplement, sous réserve d’avoir déterminé des coûts de stockage et de pénurie, il peut se révéler avantageux d’accepter des ruptures de stocks bien maîtrisées. Cette page décrit ce cas particulier où le coût de rupture de stock supporté par un article est inférieur à son coût de possession (en environnement certain).
Le graphe ci-dessous illustre l’évolution de la quantité de matière, produit ou marchandise en stock. La demande est continue et elle se traduit par des droites qui descendent en suivant toujours la même pente (sorties du stock). L’arrivée d’une livraison se traduit quant à elle par une droite verticale. En zone rouge, la demande existe mais ne peut être satisfaite pour cause de rupture de stock. Elle le sera le jour de la livraison.
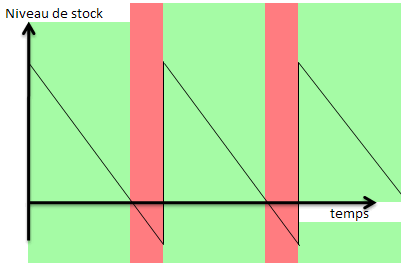
En gestion de stock, il existe trois sortes de coûts. Le coût de passation d’une commande (CPC) n’est pas impacté par la pénurie (mais le nombre de commandes l’est). Le coût de possession du stock (CPS) est supporté en zone verte tandis qu’un coût de rupture (CR) l’est en zone rouge. Ce dernier est, davantage que les deux autres, particulièrement délicat à estimer en raison de coûts cachés ou d’opportunité difficilement quantifiables.
On définit une proportion du coût de pénurie par rapport au coût global de stockage : \(p = \frac{\rm{{CR}}}{\rm{{CR}} + \rm{{CPS}}}.\)
Ce coefficient est parfois appelé taux de service. Ce terme est un peu trompeur. Cette proportion est certes liée la période durant laquelle le stock est approvisionné mais aussi aux différences de coûts unitaires (ce n'est donc pas le taux de service défini par ailleurs sur ce site).
On le démontre facilement à l’aide d’un calcul de dérivée, la quantité optimale à commander est celle qui est obtenue en multipliant \(q\) (formule de Wilson pure, sans pénurie) par la racine carrée de l'inverse de \(p.\).
Exemple
Une société commercialise des pots de XZ08 (un mystérieux produit). Le montant annuel de ventes, pour lesquelles il n’existe pas de saisonnalité, s’élève à 30 000 pots. Le coût de possession (CPS) est estimé à 10 € par pot et par an. Le coût de passation d’une commande s’élève à 170 €. Le coût d’une pénurie est quant à lui estimé à \(80\%\) du CPS. Sous quelle condition peut-on accepter la rupture de stock ?

Déterminons d’abord les quantités à commander pour qu’il n’y ait pas de rupture (modèle de Wilson pur).
\[q = \sqrt {\frac{{2{\rm{D}} \times {\rm{CP}}{{\rm{C}}_{\rm{u}}}}}{{{\rm{CP}}{{\rm{S}}_{{\rm{u(pour\;un\;an)}}}}}}} \]
\[\Leftrightarrow q = \sqrt{\frac{2 \times 30\,000 \times 170}{10}}\]
Soit environ 1 010 pots que l'on arrondira à 1 000, c'est-à-dire 30 commandes par an (une tous les 12 jours).
Le coût annuel de la gestion de stock est constitué du CPC (\(30 × 170,\) soit 5 100 €) et du CPS (stock moyen de 500, multiplié par 10 €). Soit 10 100 €.
Étudions à présent ce que coûte la gestion de stock dans l'année si l’on accepte une pénurie.
Le CPC unitaire reste le même. Le coût de rupture (CR) s’élève quant à lui à 8 € par pot.
La quantité économique à commander s’établit à (q non arrondi) :
\(q'\) \(=\) \(q \times \sqrt{\frac{10 + 8}{8}}\) \(=\) \(1\,515\) pots.
Soit vingt commandes par an, donc une tous les dix-huit jours.
Le stock maximal n’est plus de mille pots mais de \(n\) \(=\) \(1\,515 \times \frac{8}{10 + 8}\) \(\approx\) \(673\) pots.
Ceci ne représente que \(44,44\%\) environ de la quantité à commander, c’est-à-dire qu’une gestion optimale avec pénurie se traduit ici par une rupture de stock pendant \(55,56\%\) du temps !
Le coût annuel de gestion du stock se décompose de la manière suivante :
CPC : \(2 × 170\) € \(=\) \(3\,400\) €
CPS : \(\frac{673}{2} \times 10\) € \(× 44,44\%\) \(=\) \(1\,495\) €
CR : \(\frac{1\,515 - 673}{2} × 8\) € \(× 55,56\%\) \(=\) \(1\,871\) €
Total : 6 766 €, soit une économie d’environ un tiers.
Sur les dix-huit jours de la période, le stock sera approvisionné pendant huit jours et en rupture pendant dix jours.
À condition que le consommateur ou l’utilisateur puisse attendre pendant dix jours et en supposant qu’il sera immédiatement servi dès réception de la commande, une gestion qui accepte les ruptures peut être envisagée…
