Loi géométrique : définition et exemple
Quelle est la probabilité de gagner au loto alors que c’est la première fois que l’on y joue ? Et la deuxième ? Et ainsi de suite ? Voici le type de question pour laquelle la loi géométrique apporte sinon une réponse sûre (qui risque fort d’être démoralisante), du moins une probabilité (démoralisante aussi).
Une partie de cette page figure au programme de terminale générale (maths complémentaires).
Présentation
La loi géométrique est une loi de probabilité discrète qui modélise l’observation du nombre d’épreuves de Bernoulli identiques et indépendantes devant se succéder pour espérer un premier succès.
Elle n’a donc qu’un paramètre, la probabilité de succès \(p.\) De cette probabilité découle celle d’un échec, \(q = 1 - p.\) Le fait qu’une variable aléatoire \(X\) suive une loi géométrique de paramètre \(p\) s’écrit \(X \leadsto \mathscr{G}(p).\)
Soit \(n\) le nombre de tirages. La probabilité de remporter un premier succès à l'épreuve \(n\) est égale à \(P(X = n)\) \(=\) \(pq^{n-1}.\)
Attention toutefois au contexte. Si l’on considère que la première valeur de \(n\) est zéro, cette probabilité devient \(pq^n.\)
D’ailleurs il suffit d’un minimum de bon sens pour retrouver cette formule. Par exemple, la probabilité d’obtenir un succès à la cinquième épreuve s'établit à \(q × q × q × q × p.\)
Au passage, vous devinez pourquoi cette distribution est qualifiée de géométrique (suite géométrique de premier terme \(p\) et de raison \(q\).
La fonction de répartition \(F(n)\) représente la probabilité de réaliser au plus \(n\) tirages pour obtenir le premier succès (ceci n'est pas au proramme de terminale).
\(F(n)\) \(=\) \(p(X \leqslant n)\) \(=\) \(1 - q^n\)
Démonstration. Nous déduisons de \(p(X = n)\) que \(P(X \leqslant n)\) \(=\) \(\displaystyle{\sum\limits_{i = 1}^n {pq^{i-1}}}\) \(=\) \(\displaystyle{p \sum\limits_{i = 0}^{n-1} {q^{i}}}\)
Reconnaissez-vous dans cette somme celle des \(n\) premiers termes d’une suite géométrique de raison \(q\) et de premier terme 1 ? Oui ? Alors…
\(\displaystyle{p(X \leqslant n) = p \times \frac{1 - q^n}{1 - q}}\)
Et comme \(1 - q = p,\) on simplifie notre affaire en écrivant simplement \(1 - q^n.\) Démonstration pas trop douloureuse !
L’espérance est \(E(X) = \frac{1}{p}.\)
Par exemple, il faut en moyenne six essais pour obtenir un 6 avec un dé cubique non truqué (l'inverse de \(\frac{1}{6}\).)
Encore une fois, attention à la problématique. Si par exemple on s’intéresse au nombre d’échecs en excluant le succès, nous avons \(E(X) = \frac{1}{p} - 1,\) soit \(\frac{q}{p}.\)
La variance (qui n'est pas non plus au programme de terminale) : \(\rm{Var}(X)\) \(=\) \(\displaystyle{\frac{q}{p^2}}\) \(=\) \(E(X)(E(X) - 1).\)
Donc \(\sigma (X)\) \(=\) \(\displaystyle{\frac{\sqrt{q}}{p}}.\)
En revanche, pour les indicateurs de dispersion, aucun changement de formule si l’on exclut le succès.
Représentation graphique
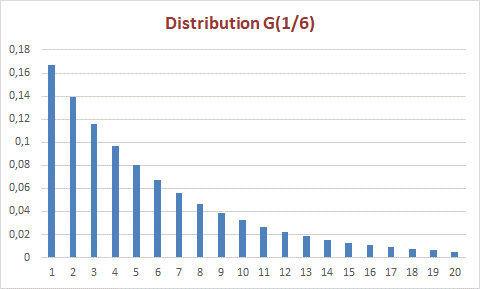
La distribution est toujours étalée à droite. Reprenons l’exemple du lancer de dé où la probabilité de succès s’établit à \(\frac{1}{6}.\) Ci-dessous, nous avons choisi de limiter le graphique à vingt lancers.
Une famille de lois sans mémoire
Comme les tirages sont indépendants, c’est comme si l'on partait de zéro à chaque nouvelle épreuve. Ce n’est pas parce qu’on a lancé un dé vingt fois sans obtenir le 6 qu’on a plus de chances d’obtenir 6 plutôt qu’une autre valeur au vingt-et-unième lancer.
Ainsi, la loi géométrique n’est autre que la version discrète de la loi exponentielle.
Remarque : la loi de Pascal décrit la situation d’attente du énième succès. La loi géométrique en est donc un cas particulier (arrêt au premier succès). Le nombre d’échecs avant le énième succès est quant à lui modélisé par la loi binomiale négative, ou loi de Polya.
Exemple
Un jardin botanique possède une plante qui fleurit une seule fois dans sa vie avant de mourir. Son espérance de vie moyenne est de 10 ans mais elle peut vivre beaucoup plus longtemps à condition de ne pas fleurir. Un botaniste doctorant cherche des signes avant-coureurs de cette floraison puisque celle-ci semble survenir de façon totalement aléatoire. Il a quatre ans devant lui, après quoi sa soutenance de thèse sera passée. Quelle est la probabilité qu’il puisse observer la plante pendant trois ans sans floraison puis que celle-ci intervienne la quatrième année ?
Nous pouvons modéliser cette situation par une loi géométrique. La probabilité de succès est \(p = 0,1\) (une année sur dix).
\(p(X = 4)\) \(=\) \(0,1 × 0,9^3\) \(=\) \(0,0729\)
Soit environ sept chances sur cent que les choses se déroulent ainsi. Comme la probabilité de cette éventualité est un peu faible, notre botaniste se dit qu'il pourrait étudier la floraison en elle-même. Quelle est la probabilité qu’il puisse l’observer au cours de ses quatre années de doctorat ?
Nous cherchons une probabilité de succès pour \(n = 1,\) \(2,\) \(3\) ou \(4.\)
\(P(X \leqslant 4)\) \(=\) \(1 - 0,9^4\) \(=\) \(0,3439.\)
La probabilité que le botaniste observe la floraison au cours des quatre années à venir s'établit à 0,3439.
Voir aussi la loi géométrique avec calculatrice.
