Kurtosis
Une série statistique ou une distribution probabiliste est habituellement résumée par un certain nombre d'indicateurs, plus ou moins nombreux en fonction du type d'étude réalisée.
Présentation
À la fin du dix-neuvième siècle, Karl Pearson avait doté les statistiques des principaux outils utilisés aujourd'hui (écart-type, histogramme...). Il s'attacha aussi à résumer le degré d'applatissement d'une distribution par un indicateur de forme (plus ou moins plate qu'une distribution normale). Et pour celà il créa le kurtosis.
Le moment d'ordre 4
Le sabir des statistiques semble constituer un obsessionnel détournement des mots les plus banals. Artistes facétieux, les statisticiens se sont notamment emparés du mot « moment » pour lui affecter un sens tout particulier (en fait le terme vient de la mécanique).
Un moment d’ordre \(k\) est l’espérance mathématique de variables aléatoires indépendantes à la puissance \(k\) (ou la moyenne de variables statistiques à la puissance \(k\) si l'on se situe dans une problématique descriptive). Si le moment est centré, c’est l’espérance des écarts entre variable aléatoire et espérance à la puissance \(k.\)
Le moment centré d’ordre 4 permet de calculer le degré d’aplatissement d’une distribution à une variable. Afin d’obtenir un nombre sans dimension, on le divise par le carré de la variance. L’indicateur obtenu est appelé coefficient d’aplatissement de Pearson, ou kurtosis.
Pour résumer : \(\mu_4 = E[(X - m)^4]\) et le coefficient \(\displaystyle{\gamma_2 = \frac{\mu_4}{\sigma^4}}\)
Le kurtosis d’une loi normale (de Gauss) est égale à 3. Certains auteurs (surtout anglo-saxons) et logiciels retranchent 3 à la forme ci-dessus, ce qui conforte la loi normale dans son rôle de « loi étalon ». Le coefficient obtenu est dit « de Fisher » (ou excess kurtosis). Comme cette option nous semble beaucoup plus pratique, c'est celle que nous retiendrons par défaut.
Précisons que le kurtosis est défini pour la plupart des lois usuelles mais qu’on l’estime aussi pour des lois empiriques (VaR de crédit, par exemple).
Un coefficient de Fisher positif traduit une distribution leptokurtique (distribution qui s’élève assez haut puis retombe assez brutalement). Le mot n’est pas facile à placer dans une conversation mais vous pouvez toujours déclarer que les ventes du tube de l’été suivront une distribution leptokurtique. Voir la courbe rouge ci-dessous.
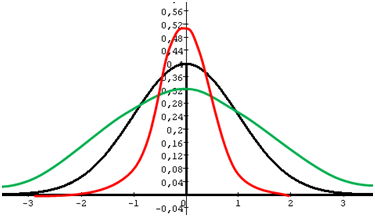
Une distribution normale est mésokurtique (en noir ci-dessus) et une distribution à « queues épaisses », dont le coefficient est négatif, habituelle dans l’étude des VaR, est platikurtique (en vert).
Attention tout de même à ne pas amalgamer cette notion avec la variance. Une distribution platikurtique n’a pas nécessairement une variance plus élevée qu’une leptokurtique.
Coefficients d’aplatissement des lois usuelles.
\(\displaystyle{\gamma_2 = \frac{1 - 6pq}{npq}}\)
\(\displaystyle{\gamma_2 = e^{4 \sigma^2} + 2^{3 \sigma^2} + 3e^{2 \sigma^2} - 6}\)
\(\displaystyle{\gamma_2 = \frac{1}{\lambda}}\)
Loi du khi² à \(n\) degrés de liberté :
\(\displaystyle{\gamma_2 = \frac{12}{n}}\)
Loi de Student à \(n\) degrés de liberté (si \(n > 4\)) :
\(\displaystyle{\gamma_2 = 3 + \frac{6}{n-4}}\)
Loi uniforme (discrète) sur \([0\,;1]\) : 1,8 (non normalisé) ou -1,2 (si normalisé).
Loi exponentielle : 9 (non normalisé) ou 6 (normalisé).
Logiciels
La plupart des logiciels fournissent par défaut le coefficient de Fisher (SAS, SPSS…).
Certains « petits » logiciels préfèrent toutefois celui de Pearson (StatCalc).
Exemple : série de notes suivant à peu près une loi normale (exemple repris en page test du khi² d'adéquation).
Extrait des résultats de XLSTAT :
La valeur -0,906 est celle qui est donnée par la fonction KURTOSIS d'Excel. On la retrouve aussi (en option) parmi les statistiques descriptives de SPSS :
Statgraphics propose une formule beaucoup plus alambiquée sur les petits échantillons (précisons que cet indicateur est biaisé sur un échantillon, à l'instar de la variance). Au-delà d'une certaine taille, l'aplatissement standardisé est égal à :
\(\displaystyle{z_2 = \frac{\gamma_2}{\sqrt{\frac{24}{n}}}}\)
En l'occurrence, il est donc égal à -1,013.
Webographie : http://mathworld.wolfram.com/Kurtosis.html
