Nombres carrés, pentagonaux et hexagonaux
Les nombres polygonaux sont fascinants. Ils sont définis comme des nombres pouvant être représentés sous forme de figures géométriques régulières, comme des triangles, des carrés ou des pentagones.
Un intérêt ancien
Leur étude remonte aux pythagoriciens, qui s'intéressaient aux propriétés de certains nombres, qu’ils figuraient avec des cailloux.
Diophante fut un mathématicien grec du troisième siècle. On a tendance à placer tous les mathématiciens grecs à peu près à la même époque, ce qui est une belle erreur : Diophante a une différence d’âge d’environ 800 ans avec Pythagore. Quoi qu’il en soit, il a écrit un livre sur les nombres polygonaux pour en énoncer des propriétés qui s’affranchissaient enfin de la géométrie.
En fait, c’est en étudiant les suites que vous avez de bonnes chances de les rencontrer.
Définition et propriétés
Un nombre polygonal de \(s\) côtés est un nombre qui peut être disposé sous la forme d'un polygone régulier ayant \(s\) côtés. La formule générale pour le énième nombre polygonal de côtés est donnée par :
\(P(s,n)=\frac{(s-2)n^2-(s-4)n}{2}\)
\(s\) représente le nombre de côtés du polygone et \(n\) est le rang du nombre polygonal dans la séquence.
Ainsi, pour \(n = 3,\) on obtient des nombres triangulaires et pour \(n = 4\) les nombres carrés (suite des carrés parfaits : 1, 4, 9, 16, 25…).
Les nombres polygonaux possèdent plusieurs propriétés intéressantes. Nous en évoquerons certaines. Par exemple, chaque nombre carré est la somme de deux nombres triangulaires consécutifs. De plus, certains nombres polygonaux apparaissent dans les solutions de problèmes de partitions et en théorie des nombres. Ils ont aussi des applications en informatique et en cryptographie, notamment dans la génération de clés et l'optimisation des bases de données.
Nombres triangulaires
Nous vous renvoyons à la page sur les nombres triangulaires pour faire leur connaissance, et en particulier de leur représentation physique. Nous ajoutons ici une démonstration et quelques propriétés.
Les premiers sont 1, 3, 6, 10, 15… (on ajoute 2, puis 3, puis 4…).
Montrons que la somme de deux nombres triangulaires consécutifs est toujours un carré parfait. Appelons \(T_n\) le énième nombre triangulaire.
D’abord, il faut se souvenir que le énième nombre triangulaire est égal à la somme des \(n\) premiers termes de la progression arithmétique.
\(T_n = \frac{n(n+1)}{2}\)
Donc :
\(T_n + T_{n-1} = \frac{n(n+1)}{2} + \frac{(n-1)(n-1+1)}{2}\)
\(\Leftrightarrow T_n + T_{n-1} = \frac{n(n+1)+n(n-1)}{2}\)
\(\Leftrightarrow T_n + T_{n-1} = \frac{n(n+1+n-1)}{2}\)
\(\Leftrightarrow T_n + T_{n-1} = \frac{n \times 2n}{2}\)
\(\Leftrightarrow T_n + T_{n-1} = n^2\)
Par ailleurs, un nombre rectangulaire est la somme de deux nombres triangulaires et un nombre pentagonal est la somme de trois nombres triangulaires.

Carl Friedrich Gauss a démontré que tout entier positif est la somme d’au plus trois nombres triangulaires.
Nombres carrés
Bien sûr, pour obtenir les nombres carrés, il suffit de multiplier les entiers par eux-mêmes. \(1 \times 1 = 1,\) puis \(2 \times 2 = 4,\) puis \(3 \times 3 = 9,\) puis \(4 \times 4 = 16,\) etc. Une autre façon est d’additionner les termes de la suite des premiers nombres impairs : \(1,\) puis \(1 + 3 = 4,\) puis \(4 + 5 = 9,\) puis \(9 + 7 = 16,\) etc.
Une petite représentation graphique pour vous en convaincre ?
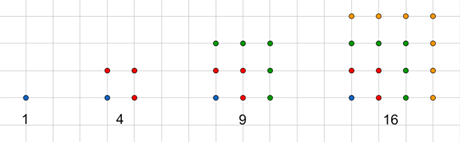
Formellement :
\(\displaystyle{n^2 = \sum_{k=1}^n(2k - 1)}\)
Par ailleurs, un nombre carré est toujours la somme de deux nombres triangulaires (refaire la démonstration ci-dessus en partant de la fin).
Autre propriété, si l’on ajoute 1 au produit de deux nombres impairs consécutifs, on obtient le carré du nombre pair situé entre eux.
\((2n-1)(2n+1) + 1\) \(=\) \(4n^2 – 1 + 1\) \(=\) \((2n)^2\)
Par exemple, \(11 \times 13 + 1 = 144,\) soit \(12^2.\)
On obtient aussi un carré en ajoutant 1 au produit de quatre nombres consécutifs.
Nombres pentagonaux et hexagonaux
Les nombres pentagonaux forment des pentagones (nous ne les avons pas représentés) : 1, 5, 12, 22, 35…
Chaque nombre pentagonal est égal au précédent majoré d’un terme de la suite arithmétique de premier terme 1 et de raison 3. Soit \(1,\) puis \(1 + 4 =5,\) puis \(5 + 7 = 12,\) puis \(12 + 10 = 22,\) etc.
Le énième nombre pentagonal est \(\frac{3n^2 - n}{2}.\)
Pour savoir si un nombre \(n\) est pentagonal, on doit vérifier que la formule suivante a pour résultat un entier :
\(\displaystyle{\frac{1 + \sqrt{24n + 1}}{6}}\)
Exemple : vérifions que 35 est pentagonal.
\(\displaystyle{\frac{1 + \sqrt{24 \times 35 + 1}}{6}}\) \(=\) \(5\)
35 est bien un nombre pentagonal (ce résultat de 5 nous indique que c’est le cinquième).
Les nombres hexagonaux sont 1, 6, 15, 28, 45… Chaque nombre est obtenu en ajoutant au précédent un terme de la suite arithmétique de premier terme et de raison 4. Soit \(1,\) puis \(1+5=6,\) puis \(6+9=15,\) puis \(15+13=28,\) etc.
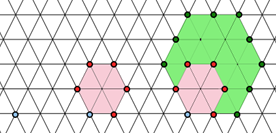
La formule générale du nombre hexagonal est \(2n^2 - n.\) Ainsi le cinquième nombre est égal à \(2 \times 5^2 - 5,\) soit 45.
