Exemple de suites adjacentes
Il était une fois un théorème sorti du cerveau d’un mathématicien qui déclara : « si les suites réelles \((u_n)\) et \((v_n)\) sont adjacentes, alors elles sont convergentes et ont la même limite » ! Abasourdi, le peuple en conclut que si l’une des suites était croissante et l’autre décroissante, la limite se trouvait forcément entre les deux… Et chacun se mit en devoir de chercher la mystérieuse limite car le théorème n’en avait pas donné l’emplacement.
Le principe
Deux suites \((u_n)\) et \((v_n)\) \((n \in \mathbb{N})\) sont adjacentes si l'une est croissante et l'autre décroissante et si leur différence \(u_n - v_n\) converge vers une limite nulle (les suites convergent et ont la la même limite).
Exemple
Cet épisode vous contera l’histoire des trois suites \((u_n),\) \((v_n)\) et \((w_n)\) définies comme suit :
\(u_{n+1} = \frac{1}{8}(5u_n + 3v_n)\) avec \(u_0 = 2.\)
\(v_{n+1} = \frac{u_n + v_n}{2}\) avec \(v_0 = 10.\)
\(w_n = v_n - u_n\)
Comme vous le constatez, elles étaient très liées. L’aventure consistait à montrer que les suites \((u_n)\) et \((v_n)\) étaient adjacentes et peut-être même trouver leur limite commune…
La première étape consista à démontrer que \((w_n)\) était une suite géométrique.
\(w_{n+1} = \frac{u_n}{2} + \frac{v_n}{2} - \frac{5u_n}{8} - \frac{3v_n}{8}\)
\( \Leftrightarrow w_{n+1} = -\frac{u_n}{8} + \frac{v_n}{8}\)
\(\Leftrightarrow w_{n+1} = \frac{1}{8}w_n\)
Ainsi, il s’agissait bien d’une suite géométrique de raison \(\frac{1}{8}\) (soit 0,125) et de premier terme \(w_0 = 10 - 2 = 8.\)
L’épreuve suivante consista à déduire que, quel que soit \(n,\) \(v_n\) était supérieur à \(u_n.\) Il fallait donc montrer que \(w_n\) était toujours positif. La tâche n’était pas insurmontable pour qui connaît la formule définissant une suite géométrique : c’est le premier terme, multiplié par la raison à la puissance \(n.\) Et comme \(8 × 0,125^n\) est toujours positif, \(v_n\) était toujours supérieur à \(u_n\)…
Fort de ses déductions initiales, le bon peuple voulut s’assurer que l’une des suites était croissante et l’autre décroissante afin de cerner le repaire de l’énigmatique limite. Pour cela, il fallut délier les suites \((u_n)\) et \((v_n).\) Ainsi isolées, elles n’offriraient aucune résistance à une minutieuse étude.
Les préparatifs furent les suivants :
\(u_{n+1} - u_n = \frac{5}{8}u_n + \frac{3}{8}v_n - u_n\)
\(\Leftrightarrow u_{n+1} - u_n = - \frac{3}{8}u_n + \frac{8}{8}v_n\)
À ce moment-là, le détachement de \(v_n\) put avoir lieu car, en observant bien, on s’aperçut que la différence entre \(u_{n+1}\) et \(u_n\) n’était autre que \(w_n × \frac{3}{8}.\) Dans la mesure où \(w_n\) était positif, chacun comprit que la suite était croissante…
Le même stratagème fut appliqué à \((v_n)\) et, après quelques péripéties, il apparut que \(v_{n+1} - v_n\) était égal à \(w_n × (-\frac{1}{2}).\) Donc, \(v_n\) était plus grand que \(v_{n+1}\), impliquant que la suite décroissait inexorablement !
Pour montrer que \((u_n)\) et \((v_n)\) étaient adjacentes, il fallait s’assurer que ce qui les séparait, c’est-à-dire \(w_n,\) devenait de plus en plus inexistant au fur-et-à-mesure que \(n\) augmentait. Le calcul de la limite à l’infini de \((w_n)\) n’était même pas nécessaire : comme \(w_{n+1} = \frac{w_n}{8},\) il était évident que cette limite était égale à zéro…
Le cadre était posé. Les suites étaient adjacentes et donc convergeaient vers la même limite. Il restait à trouver cette dernière, le théorème étant resté muet sur ce lieu secret.

Excel
Mais le peuple avait beau retourner les égalités dans tous les sens, il finissait toujours par tomber sur \(1 = 1.\) Ne trouvant pas de calcul élégant pour déterminer l’endroit où cette limite se cachait, ils utilisèrent un tableur, arme fatale s’il en est…
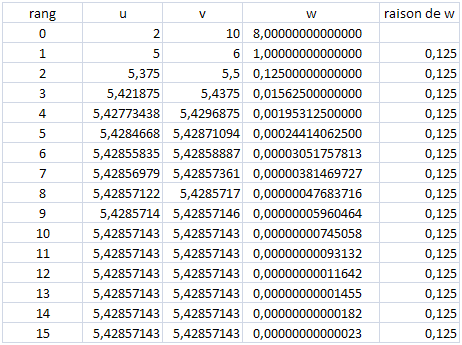
La fin justifie les moyens.
Pour compléter l'histoire, ajoutons que les suites ne sont pas toujours enchevêtrées comme celles-ci. La méthode courante consiste alors à montrer que l'une est croissante, l'autre est décroissante et la limite de la différence des deux tend vers 0 lorsque \(n\) tend vers l'infini, à l'instar d'une courbe qui tend vers une asymptote oblique... Enfin, la preuve de l'existence d'une suite adjacente peut servir à montrer qu'une suite monotone converge.
