Calculs de longueurs de sous-tangentes
Dans l'enseignement secondaire, la sous-tangente ne fait pas partie des programmes de maths. Consolons-nous, elle peut apparaître à l'occasion d'un exercice.
Celui qui suit est du niveau d'une classe de première générale. Il peut aussi servir d'introduction à un prolongement possible du programme de terminale (maths complémentaires).
La sous-tangente
Soit une fonction \(f\) continue et dérivable sur un intervalle \(I.\) Précision importante, en aucun point de \(I\) elle ne doit être nulle.
Soit dans un repère orthonormé la tangente \(T\) au point \(M\) appartenant à la courbe représentative de\(f\) sur \(I.\)
Soit \(P\) le point d'intersection entre \(T\) et l'axe des abscisses et soit \(M'\) le projeté orthogonal de \(M\) sur l'axe des abscisses.
La sous-tangente de la courbe en \(M\) est le segment \([P\, ;M'].\)
Illustration
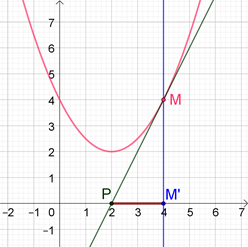
Soit la courbe représentative de la fonction \(f : x ↦ 0,5x^2 - 2x + 4\) et \(M\) son point d'abscisse 4. Sa sous-tangente en 4 apparaît ici en trait épais.
Exercice
Pour les questions qui suivent nous nous situerons sur l'intervalle \(\mathbb{R}_+^*.\)
1- Déterminer les longueurs \(OM'\) et \(PM'\) de l'exemple précédent. En déduire une relation entre elles.
2- Faire de même pour la fonction carré, la fonction inverse, la fonction cube et la fonction racine carrée. Nous appellerons \(a\) l'abscisse des points \(M\) et \(M'\) et \(p\) l'abscisse du point \(P.\)
Corrigé
1- Nous devons calculer l'équation de la tangente en 4 et pour cela déterminer la dérivée \(f'.\)
\(f'(x) = x - 2.\) Par ailleurs, \(f(4) = 8 - 8 + 4 = 4.\) Enfin, \(f'(4) = 4 - 2 = 2.\)
\(T = 4 + 2(x - 4) = 2x - 4.\)
\(M(4\, ;4)\) donc \(M'(4\, ;0).\) Quant à \(P,\) nous le trouvons en posant \(T = 0.\) Donc \(P(2\, ;0).\)
Par conséquent, \(PM' = \frac{1}{2} OM'.\)
2- Fonction carré : \(f'(x) = 2x,\) \(f(a) = a^2\) et \(f'(a) = 2a.\)
Donc \(T = a^2 + 2a(x - a)\)
\(⇔ T = a^2 + 2ax - 2a^2\)
\(⇔ T = -a^2 + 2ax\)
Déterminons \(p.\)
\(-a^2 + 2ap = 0\) donc \(p = \frac{a}{2}\)
Donc \(OM' = a\) et comme \(OP = \frac{a}{2}\) alors \(PM' = \frac{a}{2}.\)
Là encore, \(PM' = \frac{1}{2} OM'.\)
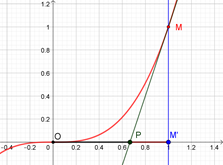
Fonction cube : \(f'(x) = 3x^2,\) \(f(a) = a^3\) et \(f'(a) = 3a^2.\)
Donc \(T = a^3 + 3a^2(x - a)\)
\(⇔ T = a^3 + 3a^2x - 3a^3\)
\(⇔ T = -2a^3 + 3a^2x\)
Déterminons \(p.\)
\(-2a^3 + 3a^2p = 0\) donc \(p = \frac{2}{3}a\)
\(OM' = a\) et comme \(OP = \frac{2a}{3}\) alors \(PM' = \frac{OM'}{3}.\)
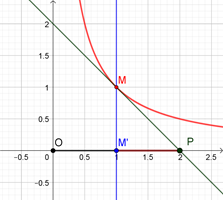
Fonction inverse : \(f'(x) = -\frac{1}{x^2},\) \(f(a) = \frac{1}{a}\) et \(f'(a) = -\frac{1}{a^2}.\)
Donc \(T = \frac{1}{a} - \frac{1}{a^2}(x - a)\)
\(⇔ T = \frac{1}{a} - \frac{x}{a^2} + \frac{1}{a}\)
\(⇔ T = -\frac{1}{a^2}x + \frac{2}{a}\)
Déterminons \(p.\)
\(-\frac{1}{a^2}p + \frac{2}{a} = 0\) donc \(p = 2a\)
\(OM' = a\) et comme \(OP = 2a\) alors \(PM' = OP - OM' = OM'.\)
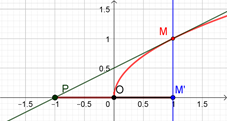
Fonction racine carrée : \(f'(x) = \frac{1}{2\sqrt{x}},\) \(f(a) = \sqrt{a}\) et \(f'(a) = \frac{1}{2 \sqrt{x}}\)
Donc \(T = \sqrt{a} + \frac{1}{2 \sqrt{a}} (x - a)\)
\(⇔ T = \frac{2a + x - a}{2 \sqrt{a}}\)
\(⇔ T = \frac{x + a}{2 \sqrt{a}}\)
\(⇔ T = \frac{1}{2 \sqrt{a}}x + \frac{\sqrt{a}}{2}\)
Déterminons \(p.\)
\(\frac{p + a}{2 \sqrt{a}}= 0\) (cette expression est plus pratique), donc \(p = -a\)
\(OM' = a\) et comme \(OP = a\) alors \(PM' = 2OM'.\)
Note : cet exercice illustre une propriété des fonctions puissances, à savoir \(PM' = \frac{1}{|n|}\) (n'oublions pas que \(\frac{1}{x} = x^{-1}\) et \(\sqrt{x} = x^{0,5}\)). Vous pouvez le compléter en réalisant l'exercice sur sous-tangentes avec équations différentielles (niveau terminale).
