Usufruit, nue-propriété et taux de rentabilité actuariel
Non, non, vous n’êtes pas sur un site juridique. Les notions d’usufruit et de nue-propriété sont juste les expressions habituellement retenues dans le cadre de l’évaluation du prix théorique d’une créance à revenu prédéterminé…
Usufruit et nue-propriété
La nue-propriété est la valeur actuelle du capital qui n’est pas encore amorti.
L’usufruit est la valeur actuelle des intérêts pas encore versés.
Le prix théorique de la créance globale est la somme de ces deux éléments. On l'établit donc par un calcul actuariel.
Ces termes sont applicables à un emprunt indivis comme à un emprunt obligataire ou à une obligation vivante.
Une unité monétaire est constituée d’un usufruit unitaire \(u\) et d’une nue-propriété unitaire \(p.\)
\(u\) est égal à l’usufruit \(U\) divisé par la valeur du coupon tandis que \(p\) est égal à la nue-propriété \(P\) divisée par le montant de l’emprunt (ou, s’il existe une prime de remboursement, à ce qu’il reste à amortir divisé par la valeur de remboursement de l’obligation). Dans le cas d'une rente, \(p = 0.\)
Cliquez sur l'exemple de prix de souscription si vous souhaitez en savoir davantage.
Le taux actuariel
Qu’est-ce qu’un taux actuariel ? C’est le taux qui permet à tout moment d’estimer la rentabilité d’une créance et en particulier d’une obligation.
Il s’agit d’un taux d’actualisation, c’est-à-dire qu’il tient compte des versements attendus et que ceux-ci doivent égaler le prix de l’obligation à la date de calcul lorsqu’on leur applique ce fameux taux. Si l'emprunt est in fine, \(p = (1 + k)^{-n}\) avec \(k =\) taux d'actualisation.
Si l'on utilise la nue-propriété et l'usufruit unitaires, on observe la plupart du temps l'égalité suivante : \(k = \frac{1 - p}{u}\)
Du point de vue de l’emprunteur, c'est en revanche un taux de revient (qui tient compte des frais, notamment d’émission).
La notion de taux actuariel est donc importante, bien davantage que celle de taux nominal, du moins pour quiconque souhaite conserver ses obligations un certain temps...
À l’émission, le taux actuariel est appelé TRABE (Taux de Rendement Actuariel Brut à l’Émission). Il est précisé dans le contrat d’émission. S’il n’existe ni prime d’émission ni prime de remboursement, c’est tout simplement le taux nominal.
Le taux actuariel \(k\) d’une obligation égalise donc le prix théorique de celle-ci à un moment donné (\(P_0\)) avec les flux à venir \(c\) (coupons) et \(R\) (valeur de remboursement). La formule suivante détaille les annuités :
\(P_0\) \(=\) \(\frac{c}{1 + k}\) \(+\) \(\frac{c}{(1 + k)^2}\) \(+\) \(...\) \(+\) \(\frac{c + R}{(1 + k)^n}\)
Ce taux peut être calculé brut (TAB) ou net (TAN) des divers prélèvements obligatoires. Par ailleurs, son rôle s'étend tout a fait aux actions (Cf. le modèle de Durand).

Exemple théorique
Soit le diagramme des flux suivant :
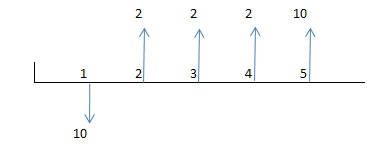
Le taux actuariel est solution de l’équation :
\(\frac{10}{1+k}\) \(-\) \(\frac{2}{(1 + k)^2}\) \(-\) \(\frac{2}{(1 + k)^3}\) \(-\) \(\frac{2}{(1 + k)^4}\) \(-\) \(\frac{10}{(1 + k)^5}\) \(=\) \(0\)
Le calcul nécessite une calculatrice ou un logiciel. Sans avoir recours à une calculatrice financière mais avec une simple TI-82 STATS que possèdent la plupart des lycéens et étudiants, on trouve \(16,0557\%\) (fonction irr sur une version anglaise ou tauxRi sur une française ; pas besoin de formule, le diagramme des flux suffit). Avec Excel, on utilise la fonction TAUX si les annuités sont constantes. Sinon, on utilise TRI (c'est toutefois plus compliqué si les périodes sont inégales). Pensez à entrer les remboursements en valeurs négatives.
Les calculs « manuels » sont tombés en désuétude. Nous vous renvoyons donc aux ouvrages de mathématiques financières pour en savoir davantage là-dessus si vous le souhaitez…
Soyons moins théoriques
Cependant, un taux varie selon les échéances. Ce n'est pas le cas dans l'exemple ci-dessus. Qu'il soit à un ou cinq ans, on l'a établi à \(k = 16,0557\%.\) C'est comme si les courbes de taux n'étaient que de banales droites horizontales...
Concrètement, ce taux \(k\) sera solution d'une équation dont le sens est assez intuitif. C'est une sorte de moyenne de différents taux, en principe de plus en plus élevés au fur-et-à-mesure que l'échéance est lointaine. Dans la première équation ci-dessus, il suffit de remplacer \(P_0\) par la même expression qu'à droite mais avec les taux différents observés sur les courbes.
Le taux actuariel peut être considéré comme un taux effectif de rentabilité à condition de réinvestir les coupons perçus au même taux (illusoire en pratique).
On se fonde sur les mêmes hypothèses et l'on procède au même type de calcul pour déterminer la rentabilité d'un investissement non financier. Le taux actuariel qui correspond à une valeur actuelle nette (VAN) nulle est appelé taux interne de rentabilité (TIR). Les fonctions de calcul sur tableur ou sur calculatrice sont les mêmes que pour établir le taux actuariel d'un investissement financier.
