Annuités constantes et géométriques
Ce n'est pas pour vous embrouiller mais sous ce titre d’« annuités » se cachent aussi des mensualités. La périodicité ne modifie en rien les principes de calcul.
Annuités
Le terme annuité est une notion de mathématiques financières qui caractérise plusieurs types d'applications. Les annuités peut être générées par un investissement financier et elles comprennent alors une part de remboursement du capital (amortissement) ainsi qu'une part d'intérêt (plus éventuellement une assurance). Elles peuvent aussi prendre la forme d'un versement périodique de rente, donc sans remboursement de capital. Une illustration par un prêt immobilier qui détaille la décomposition entre intérêts et remboursement figure en page d'emprunt à annuités constantes.
Par rapport à un plan de remboursement (ou de placement), l’annuité peut être anticipée, de début de période, à terme échu ou différée.
Enfin, les annuités peuvent être constantes ou en progression géométrique (voire quelconques ou en progression arithmétique mais ces situations ne seront pas abordées ici).
Voici deux situations simples où interviennent des annuités constantes. La première décrit une rente et la seconde s'intéresse au montant global des annuités d'emprunt.

Annuités constantes
Le total des remboursements ou des revenus d'une rente suit une progression arithmétique ayant pour raison le montant de l'annuité (c'est évident).
Notons \(V_0\) la valeur actuelle, \(V_n\) la valeur acquise à la date \(n\) et \(a\) le montant de l’annuité. Comme toujours, \(i\) est le taux d’intérêt (ou le taux actuariel lorsque les annuités sont des rentes). Si les annuités sont à termes échus, nous aurons (moins évident) :
\(V_0 = a \frac{1 - (1+i)^{-n}}{i}\) et \(V_n = a \frac{(1+i)^n - 1}{i}\)
Attention, si les annuités sont à terme à échoir, il convient de multiplier ces quotients par \(1 + i.\)
Avouez-le, vous souhaitez des exemples.
Vous versez 2 000 euros chaque année pendant dix ans sur un support qui vous rapporte \(4\%\) par an. Formule des intérêts composés. Versements en début de période. Voici le détail des \(V_n\) sur feuille de calcul :
Avec Excel, on obtient directement ce résultat par =VC(0,04 ;10 ;-2000 ;;1). Le premier terme de la fonction est \(i,\) le deuxième est le nombre de versements, le troisième est affecté d’un signe négatif car Excel raisonne en remboursements et non en placements, le quatrième (valeur actuelle) est ici omis et le dernier (1) renseigne un « début de période » (0 ou rien si fin de période).
Autre exemple, celui d’un remboursement. Vous empruntez 100 000 dollars au taux annuel de \(6\%,\) que vous remboursez par mensualités constantes (dès le premier mois) sur 3 ans. À combien s’élève chaque mensualité ?
Il s’agit cette fois de déterminer le \(a\) de la formule \(V_0.\) On cherche d’abord le taux équivalent mensuel \(i\) qui est une moyenne géométrique. C’est la racine douzième de 1,06 moins 1. On trouve \(0,486755\%.\)
\(V_0\) est égal à 100 000 et \(n = 36.\) Supposons la situation classique d’un remboursement en fin de période. Le résultat est alors $3 035. Sans connaître la formule on peut là aussi utiliser Excel, cette fois à l’aide de la fonction VPM. Notons au passage qu’en multipliant cette somme par 36, on obtient $109 260, soit un coût du crédit de $9 260.
Annuités en progression géométrique
Une progression géométrique permet de prendre en compte une possible inflation ou l’accroissement d’activité d’une entreprise.
Théoriquement, la valeur actuelle et la valeur acquise sont liées par une banale formule de suite géométrique, \(V_n = V_0 (1 + i)^n.\) La raison est alors égale à \(1 + i\) et le premier terme \(V_0\) représente \(n\) fois la première annuité (du moins si les annuités sont de début de période ; sinon, divisez par \(1 + i\). Par conséquent, si \(a\) est la première annuité, \(V_n = na(1 + i)^{n-1}\) lorsque les annuités sont à terme échu et \(V_n = na(1 + i)^{n}\) lorsqu'elles tombent en début de période.
En pratique la raison de la suite diffère de \(1 + i.\) Elle représente un taux d’actualisation. Ce peut être un taux d’inflation estimé ou quelque chose de plus subjectif, incluant une prime de risque et le principe de préférence pour jouissance immédiate. Bref, un joyeux fourre-tout parfaitement critiquable mais dont l’existence doit être prise en considération. Ce peut aussi être un taux de revalorisation.
Si les annuités sont à termes échus, la valeur acquise est la suivante :
\(V_n = a \frac{(1 + i)^n - q^n}{1 + i - q}\)
Lorsque les termes sont à échoir, multipliez par \(1 + i\) pour tenir compte de la période supplémentaire.
La valeur actuelle se présente ainsi :
\(V_0\) \(=\) \(\frac{a}{(1 + i)^n} \times \frac{(1 + i)^n - q^n}{1 + i - q}\)
Là encore, multipliez par \(1 + i\) si les annuités sont de début de période (c’est-à-dire que le dénominateur est élevé à la puissance \(n - 1.\)
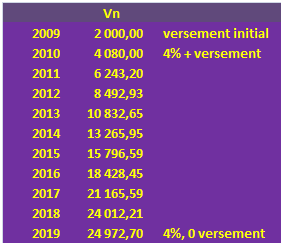
Exemple : vous placez annuellement une somme durant cinq ans. Le premier versement est de 10 000 dirhams et les suivants sont basés sur un taux d’actualisation, ou d’inflation, de \(6\%.\) Les intérêts sont versés en fin de période, au taux de \(5\%.\) Quelle sera la valeur acquise au bout des cinq ans ?
Réponse :
\(V_5\) \(=\) \(10\,000 \frac{1,05^5 - 1,06^5}{1 + 0,05 - 1,06}\) \(=\) \(61\,944\) dh.
Vérifions avec le logiciel CalcFinance. Menu Calculs financiers puis Conseiller épargne. Montant initial de l’épargne égal à zéro. Cocher Indexer les versements sur l’inflation et Versement en fin de période. Le renseignement des autres paramètres va de soi.
Extrait d’un état de sortie du logiciel (Plan d’épargne) :