Test du khi-deux d'indépendance
Un grand classique de l'analyse d'une distribution à deux variables...
Données
Vous savez ce qu’est un tableau de contingence ? Exact, c’est un tableau à double entrée dont les cellules indiquent un décompte (soit deux variables qualitatives ayant chacune plusieurs modalités, soit deux variables quantitatives présentées en classes si elles sont continues, soit un mix des deux). Voici un exemple de tableau de contingence indiquant des quantités de CD vendus sur quatre points de vente en fonction de leur style musical :
| Point de vente | Clas-sique | Variété | Rock | Électro | Jazz et blues |
| Paris | 21 | 340 | 46 | 210 | 9 |
| Lyon | 15 | 150 | 20 | 110 | 5 |
| Marseille | 17 | 180 | 19 | 99 | 6 |
| Bruxelles | 22 | 175 | 22 | 187 | 6 |
Analyse
Nous souhaitons savoir si, compte tenu de leur emplacement, ces points de vente attirent ou non des clientèles différentes (sans supposer de lien de causalité ; nous serions alors dans le cadre d’une association asymétrique). Sur un total de 1 659 CD, la part de chaque style selon le point de vente s’établit donc comme suit :
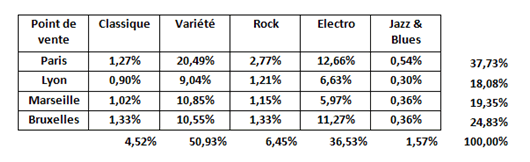
En-dehors du tableau sont indiquées les fréquences marginales, en lignes et en colonnes.
Si les styles étaient répartis de la même façon quel que soit le point de vente, l’effectif de chaque case du tableau serait égal au produit des fréquences observées sur les deux modalités étudiées, appliqué à l’effectif total.
Ainsi, Paris-Classique \(=\) \(4,52\% × 37,73\% × 1\,659\) \(=\) \(28,3.\)
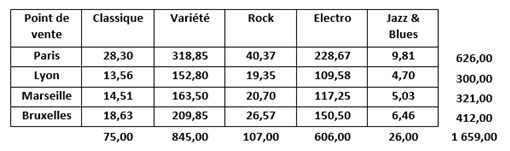
La problématique se résume à un test : peut-on accepter l’hypothèse H0 selon laquelle cette distribution théorique n’est pas significativement différente de la distribution observée ? Pour répondre à cette question, on construit un indicateur d’écart. Appelons-le \(D^2\) (son nom n’est jamais le même selon les ouvrages). Ce sera la somme, pour chaque croisement de modalités, des écarts élevés au carré et rapportés à l’effectif théorique. On ne le démontrera pas ici mais vous pouvez nous croire sur parole, cette somme suit une loi du \(\chi ^2\) à \((I - 1)(J - 1)\) degré(s) de liberté (\(I\) étant le nombre de lignes du tableau de contingence et \(J\) le nombre de colonnes).

Remarquons au passage que, si l’on peut théoriquement procéder à un test du \(\chi ^2\) sur un tableau de quatre cases, on préfère dans ce cas opter pour un test de comparaison de proportions si l'effectif le permet. Le \(\chi ^2\) établi sur un seul degré de liberté est surestimé et on le corrige généralement (correction de Yates, voir le test de la médiane).
Si l’on note \(T\) l’effectif théorique et \(O\) l’effectif observé, on résume :
\(D^2 = \sum \frac{(O_{ij} - T_{ij})^2}{T_{ij}}\)
\(\Leftrightarrow D^2 = \sum \frac{O_{ij}^2}{T_{ij}} - N\)
et \(D^2 \leadsto \chi_{(I-1)(J-1)}^2\)
Petite précision : en principe, on ne conserve pas d'effectif théorique inférieur ou égal à 5. Or, dans notre exemple, nous en avons un de 4,7… Mais soyons cool, nous n’en sommes pas très loin et il ne s’agit que d’une seule case sur 20… Si le tableau avait été plus petit, il aurait été préférable soit de regrouper le style « jazz & blues » avec, par exemple, le rock, soit d’utiliser une autre méthode que le \(\chi ^2.\)
Il existe plusieurs statistiques pour évaluer l’indépendance ou l'association entre modalités de variables.
On pourrait comparer D² à sa valeur critique dans une table du \(\chi ^2,\) en fonction du nombre de degrés de liberté (ddl) et du risque d’erreur accepté. Toutefois, les logiciels nous fournissent directement la probabilité que le \(\chi ^2\) soit supérieur ou égal à D² (p-value). Supposons qu’on accepte un risque d’erreur de 5 %, il suffit alors de comparer la probabilité obtenue à 0,05. Dans notre exemple, elle est de 0,007 (pour un \(\chi ^2\) à 12 ddl égal à 27,24). On peut donc supposer que les points de vente n’ont pas la même clientèle et que les petites différences ne proviennent pas d’une fluctuation d’échantillonnage.
Limites
Malgré sa popularité, le \(\chi ^2\) montre des insuffisances et c’est pourquoi tous les logiciels de statistiques lui joignent d’autres statistiques plus robustes, à l’image de Tanagra (ci-dessous). Notamment, le \(\chi ^2\) est sensible aux effectifs : à titre d’exemple, ce test peut nous conduire à rejeter l’indépendance mais, si l’on multiplie toutes les cases du tableau par 10, ce même test nous la fera accepter.
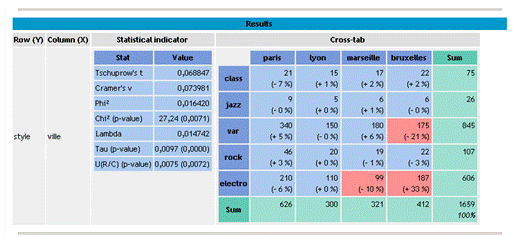
Un exemple de \(\chi ^2\) appliqué au scoring est donné pour « survoler » quelques sorties de logiciels.
Enfin, si l’on analyse un très grand tableau de contingence ou si l’on souhaite visualiser graphiquement les proximités, on procède plutôt à une AFC.