Comparaison de proportions (échantillons indépendants)
Voici un test paramétrique courant qui permet de prendre une décision après avoir comparé deux échantillons aléatoires, par exemple dans le cadre d'une étude de marché ou d'un audit social. Les contrôles de qualité, grands consommateurs de tests, l'utilisent également. Sans parler des domaines qui sortent du champ de la gestion (biostatistiques, par exemple).
Modalité booléenne
Qu'est-ce qu'une proportion ? C'est la part estimée de la population qui possède telle modalité d'une variable qualitative. On raisonne en binaire. Le partage est parfois simple (homme ou femme, par exemple). Mais si l'on teste un produit pour faire pousser les cheveux, on doit classer les résultats en deux catégories, succès et échec. Peu importe que l'échec se traduise par une absence de résultat, un résultat insuffisant ou une calvitie totale... Ni nuance, ni modalités multiples ! On considérera que l'on étudie des proportions de succès.
Estimation
On estime une proportion avec une fréquence observée.
Comme en l'occurrence on compare deux échantillons aléatoires, leurs deux fréquences empiriques de succès s'apparentent à des probabilités sur un certain nombre d'épreuves de Bernoulli et se situent dans des intervalles de confiance.
Nos échantillons doivent répondre à quelques critères. Leurs effectifs doivent en effet être supérieurs à 30 et, nous l'avons vu, être obtenus par sondage aléatoire. On trouve chez certains auteurs d’autres conditions plus restrictives (voir le test de conformité d’une proportion).
Compte tenu de ces précautions, on peut supposer que les probabilités de succès suivent une loi normale dont l'espérance serait la proportion \(p\) et dont l'écart-type serait :
\[\sigma = \sqrt{\frac{p(1 - p)}{n}}\]
Test
Tester une différence de proportions entre deux populations revient à vérifier si cette différence suit une loi normale de moyenne nulle (donc centrée). C’est l’hypothèse H0 du test. Si l'on réduit cette différence en la divisant par son écart-type, on obtient une variable aléatoire qui suit une loi normale non seulement centrée mais réduite.
\[\frac{p_1 - p_2}{\sqrt{\frac{p_1(1 - p_1)}{n_1} + \frac{p_2(1 - p_2)}{n_2}}} \leadsto \mathscr{N}(0\,;1)\]
Ainsi on compare la valeur \(t\) de la loi normale centrée réduite (c'est-à-dire 1,96 si l’on utilise le classique intervalle de confiance bilatéral de \(95\%\) à cette statistique. Notez que cette dernière peut être formalisée ainsi :
\[\frac{|p_1 - p_2|}{\sqrt{p(1 - p) \left(\frac{1}{n_1} + \frac{1}{n_2} \right)}}\]
Dans cette formule, \(p\) est la moyenne pondérée des deux fréquences observées, \(n_1\) et \(n_2\) sont les effectifs des deux échantillons. Rappelons que sous H0, \(p_1 = p_2 = p.\) Nous avons ajouté la valeur absolue car, si le test est unilatéral, on compare bien une valeur positive à la valeur indiquée dans une table de la loi normale.
Note : une comparaison de deux échantillons très petits s'effectue quant à elle avec le test exact de Fisher. En revanche, le test de proportions est en concurrence avec le test d’indépendance du khi² établi à partir d'un tableau de contingence \(2 × 2.\)
Exemple
Le statisticien RH s'intéresse à l’indicateur jours de maladies + accidents du travail du bilan social de deux filiales de sa société. Ce dernier s'analyse au regard d'un nombre de jours théoriquement travaillés :

Note : dans cet exemple, nous ne comparons pas deux échantillons mais deux sous-populations. Ce n'est pas très gênant. Le nombre de jours de maladie est bien une variable aléatoire.

La différence semble réelle (\(5,7\%\) contre \(6,1\%\). Peut-on considérer qu’il s’agit d’une simple fluctuation statistique avec un niveau de confiance de 0,95 ?
L’hypothèse H0 à tester est que les deux proportions sont identiques au seuil de \(5\%\) (test bilatéral).
\(\left\{ {\begin{array}{*{20}{c}} {H0: p_1 = p_2}\\ {H1: p_1 \ne p_2} \end{array}} \right.\)
Illustration didactique d’un traitement avec Excel (les logiciels de statistiques permettant rarement un traitement rapide à partir d'un tableau déjà construit) :
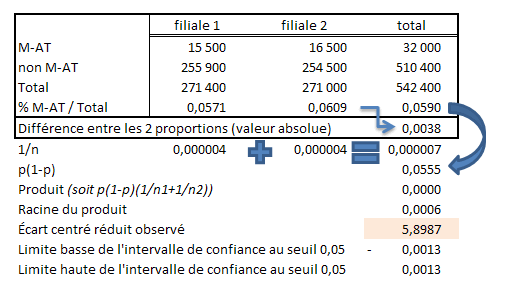
On voit qu'il est inutile de recourir à un logiciel spécialisé, pour peu que l’on s’en tienne aux niveaux de confiance habituels. Vous pouvez sauvegarder une feuille de calcul avec toutes les formules qui permettent de comparer les hypothèses et vous en servir chaque fois qu’un test de fréquence doit être réalisé. En pratique, ouvrir le fichier, modifier quatre cellules et admirer le résultat doit vous prendre moins de dix secondes…
Les étapes de calcul sont particulièrement détaillées dans le tableau. La conclusion apparaît sous deux formes.
Première forme, la ligne « Écart centré réduit » correspond au rapport indiqué plus haut. La valeur 5,8987 est supérieure à 1,96 et on rejette H0, considérant que l’écart des journées de maladies et d’accidents du travail n'est pas dû à une simple fluctuation d'échantillonnage.
La seconde façon de lire le résutat consiste à utiliser l’intervalle de confiance (deux dernières lignes du tableau). On vérifie alors si la différence observée de 0,0038 se trouve dans cet intervalle, ce qui n'est pas le cas ici.
Prudence...
Pour terminer, précisons que ce test ne s'applique pas aux échantillons appariés. Pour estimer si un même échantillon montre une évolution significative de proportions lorsqu'on l'étudie à deux instants différents, il y a le test de McNemar.
