Caractères continus
Cette page donne une première approche des séries statistiques continues. Elle fait suite à la page sur les séries statistiques, qui traite plus particulièrement des variables discrètes.
De quoi s'agit-il ?
Une variable est dite continue lorsqu’elle peut prendre une infinité de valeurs. En pratique, il ne s’agit pas d’une infinité puisque les statistiques sont établies sur une variable mesurée et qu’aucune mesure n’a la précision de l’infiniment petit ! On considère donc une variable comme continue dès lors qu’on lui attribue un grand nombre de valeurs possibles (dans les exercices, les énoncés ne laissent de toute façon aucun doute).
Analyse statistique
Pour pouvoir analyser la série statistique, on doit définir des classes de valeurs. Ce sont des intervalles qui se suivent et qui englobent toutes les valeurs de la série. Ces intervalles sont semi-ouverts. La borne basse est comprise et la borne haute est exclue. La différence entre les deux bornes est appelée l’amplitude (ce terme n’est pas exigible au programme de seconde mais comme il est bien pratique, nous l’employons quand même).
![]()
Sur la série ci-dessus, l’amplitude de chaque classe est de 200, sauf pour la dernière classe où elle est de 400. En effet, il n’est pas obligatoire de toujours prendre la même. Il est même préférable que celle-ci soit plus large lorsque l’effectif devient peu nombreux.
Pour calculer une moyenne, il faut retenir le centre de chaque classe. Ceci revient à utiliser le tableau suivant :
![]()
On se retrouve alors dans la situation d’une série discrète. Le calcul « manuel » des centres de classe n’a rien de compliqué mais il peut aussi être déterminé avec la fonction statistique de la calculatrice. La détermination d’une moyenne nécessite alors quatre colonnes au lieu de deux. La première (L1) est celle des bornes inférieures de chaque classe, la deuxième (L2) est celle des bornes supérieures, la troisième (L3) est calculée, soit (L1 + L2) / 2 (voir ci-dessous).
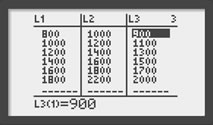
La dernière (L4) est celle des effectifs. La moyenne est établie comme indiqué sur la page série statistique mais avec L3 et L4.
La médiane et les quartiles se déterminent grâce aux fréquences cumulées.

Pour connaître la médiane, il faut sélectionner la valeur qui correspond à la fréquence cumulée de 0,5 (0,25 pour le premier quartile et 0,75 pour le troisième). On voit ici que la classe médiane est \([1\,200 -1\,400[\) puisqu’en-dessous de 1 200 nous trouvons \(30\%\) de l’effectif et qu’en-dessous de 1 400 il s’élève à \(54\%.\) La classe médiane est donc \([1\,200 - 1\,400[.\)
L’estimation d’une VALEUR médiane peut être réalisée par le calcul mais, bien que l’opération ne soit pas difficile, on demande aux élèves de seconde de l’estimer à partir du polygone des fréquences cumulées (et encore, c'est plutôt d'un exercice d'exploration puisque l'estimation de la valeur médiane d'une série continue ne figure pas au programme).
On utilise un repère dont l’axe vertical est celui des fréquences cumulées et l’axe horizontal celui des valeurs du caractère. Il faut alors indiquer par des points les fréquences cumulées qui correspondent aux extrémités de classe puis relier ces points par des segments de droites (on obtient une fonction affine par morceaux). Le tableau de valeurs qui permet de tracer la « courbe » est le suivant :
| x | y |
| 800 | 0 |
| 1000 | 0,12 |
| 1200 | 0,30 |
| 1400 | 0,54 |
| 1600 | 0,88 |
| 1800 | 0,96 |
| 2200 | 1,00 |
Ladite courbe est en principe réalisée à la règle. Ci-dessous, elle a été construite sur WxGéometrie (aujourd'hui Géophar). Ce logiciel est très pratique puisqu’il trace la construction de la médiane (en rouge) et celle des quartiles Q1 et Q3 (en pointillés bleus). On constate donc que la médiane s’établit à 1 367. Il s'agit d'une estimation puisqu'on suppose que la répartition des valeurs est linéaire au sein de chaque classe. Une supposition très forte car c'est rarement le cas.
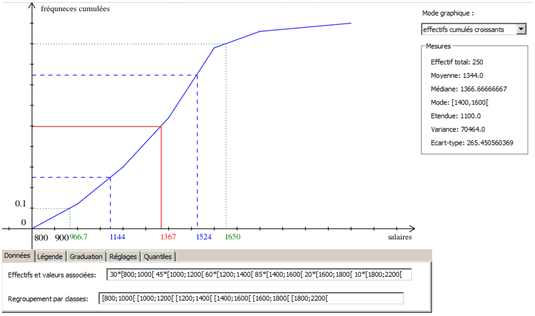
L’étendue de la série est égale à \(2\,200 - 800 = 1\,400.\) Cette information n’a pas grand intérêt, d’autant que l’on ignore sur quels critères les bornes extrêmes ont été choisies.
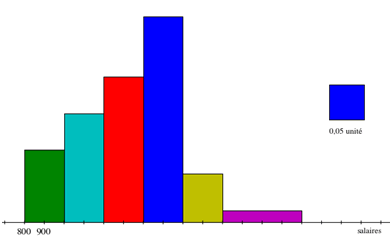
Graphes
La distribution d’une série continue se présente graphiquement par un histogramme. La construction manuelle d’un histogramme n’est pas une partie de plaisir lorsque les classes ont des amplitudes différentes puisque ce sont les aires qui sont proportionnelles aux effectifs et non la hauteur des barres. Dans notre exemple, la conversion est un jeu d'enfant puisque seule la dernière classe a une amplitude différente des autres. Comme elle est deux fois plus large que les autres, il faut diviser la hauteur de la barre correspondante par 2.

Ci-dessous, WxGéométrie n’indique pas l’axe vertical. Pour illustrer le principe de proportionnalité des aires, il faut comparer l’avant-dernière barre qui a une hauteur de 20 avec la dernière barre qui n’a pas une hauteur de 10 mais de 5.