Loi gamma, loi d'Erlang
En 1894, Karl Pearson publia une séries de courbes pour modéliser des distributions, notamment asymétiques. Celles-ci pourraient alors s'appliquer à des phénomènes aléatoires. Parmi celles-ci, la distribution gamma.
C’est un euphémisme de dire que la loi gamma n’est pas la plus célèbre des lois de probabilité. Comme ses domaines d’utilisation sont assez pointus, elle n’est enseignée que tardivement dans les cursus… Elle est notamment utilisée en fiabilité (avec usure) et en psychologie (délais avant rechute, par exemple). Mais sa singularité tient aussi aux liens qui existent entre elle et d’autres lois de probabilités.
Présentation
L’expression de sa fonction de densité (continue) fait intervenir la fonction gamma. La version « généralisée » est la suivante, pour \(a\) et \(b\) réels strictement positifs.
\(f(x)\) \(=\) \(\displaystyle{\frac{1}{\Gamma (a)} \times \frac{1}{b^a} x^{a-1}e^{- x/b}}\)
\(a\) est un paramètre de forme (shape) généralement supérieur à 1 tandis que \(b\) est un paramètre d’échelle (scale). Sur d’autres documents que celui-ci, vous trouverez peut-être une expression différente de cette fonction, avec un paramètre d’échelle égal à \(\frac{1}{b}.\)
L’espérance est égale à \(ab,\) la variance est \(ab^2\) et le mode s’établit à \((a - 1)b.\)
Lorsque \(a\) est un entier, la loi gamma est habituellement surnommée loi d’Erlang.
Propriété
Additivité : si deux variables aléatoires (v.a) suivent chacune une loi gamma de même paramètre d’échelle, la somme des deux suit une loi gamma dont le paramètre de forme est égal à la somme des deux paramètres de forme des lois initiales.
Cas particulier
Si \(a = 1\) et \(b = \frac{1}{λ},\) elle n’est autre que la loi exponentielle de paramètre \(λ.\)
Du coup, on voit bien que si l’on additionne des v.a. exponentielles, on ne peut plus décrire cette somme par une loi exponentielle mais par une loi gamma dont le paramètre de forme \(a\) est égal au nombre de v.a additionnées. D’où l’utilité de la loi d’Erlang dans les processus de Poisson. Rappelons que ces processus décrivent des évènements qui surviennent successivement mais qui sont espacés par des durées imprévisibles. Chaque durée obéit donc à une loi exponentielle. Comme cette loi n’est pas additive, une suite de plusieurs périodes aléatoires s’étudie bien avec une loi d’Erlang… Cette propriété lui vaut d’être utilisée dans la gestion du télétrafic, par exemple pour déterminer l’effectif optimal d’un centre d’appels téléphoniques ou le nombre de canaux à ouvrir dans une station GSM. Ces applications, dont la description dépasse le champ de ce site web, utilisent en fait des formules dérivées de la loi d’Erlang (Erlang-B avec perte des appels non aboutis et Erlang-C avec attente jusqu’au service).

Forme normalisée
Mais revenons au cas général où \(a \ne 1\) et où la durée de vie est plus ou moins prévisible. On emploie beaucoup la forme « normalisée » de la loi gamma, où \(b = 1.\) L’expression de la fonction est déjà moins impressionnante.
\(f(x)\) \(=\) \(\displaystyle{\frac{1}{\Gamma (a)} x^{a-1}e^{-x}}\)
Comme on le déduit facilement de l’espérance et de la variance de la forme non normalisée (vues plus haut), le paramètre \(a\) est ici égal à l’espérance mais aussi à la variance. On retrouve cette fameuse identité dans la loi de Poisson dont la loi gamma normalisée en est, ni plus ni moins, la version CONTINUE…
Loi gamma et khi²
Autre lien de parenté à signaler, cette fois avec la loi du khi². Si \(x\) suit une loi gamma normalisée de paramètre \(a,\) alors :
\(\displaystyle{2x \leadsto \chi^2_{2a}}\)
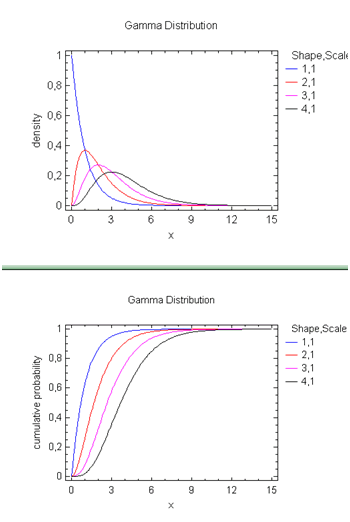
Représentations graphiques
Voici quelques courbes de densité de probabilité de la loi normalisée et au-dessous, les courbes représentatives des fonctions de répartition (réalisation sur Statgraphics Centurion) :