Loi de Pareto : formules et exemples de courbes
Vilfredo Pareto a beaucoup apporté à l’économie politique comme à la sociologie. Cependant, son nom est surtout resté associé à une « règle » issue de l’une de ses observations. Il avait remarqué que \(20\%\) des habitants d’un pays comme l’Italie ou la Suisse possédaient \(80\%\) de sa richesse. C’est le principe de Pareto : \(20\%\) des causes produisent \(80\%\) des effets. Et comme cette proportion se vérifie dans un grand nombre de domaines, il n’en fallait pas davantage pour formaliser ce type de problématique.
Loi de Pareto
Cette formalisation se traduit par une loi de probabilité. Cette loi, dite de Pareto, va au-delà du simple constat énoncé ci-dessus en permettant de répondre à la question suivante : quelles proportions d’une population se situent théoriquement en-deçà et au-delà d’un certain seuil ?
L’expression de sa densité de probabilité comprend deux paramètres. Pour les déterminer, il faut bien sûr se fonder sur l’observation du phénomène à modéliser. Mais bien souvent, on ne va pas aussi loin et l’on utilise simplement un graphique représentant les données, à l’instar d’un abaque ou d’une courbe de Lorenz. Cette approche empirique est illustrée en page de courbes 80-20 et ABC, en l’occurrence dans le cadre d’une gestion de stocks.
Pour qu’un modèle soit considéré comme prédictif, il faut déterminer au mieux ses paramètres et s’assurer que le type de loi de probabilité à été judicieusement choisi. Grâce aux formules mathématiques qui vous sont présentées ci-dessous, votre logiciel statistique pourra alors établir des prévisions.
Quels sont ces paramètres ? L’un est un paramètre de forme, \(α > 0.\) C’est l’indice de Pareto. L’autre est un paramètre d’échelle mais aussi d’origine (valeur minimale), \(x_0 > 0.\)
La densité de probabilité s’exprime ainsi :
\(f(x)\) \(=\) \(\left\{ {\begin{array}{*{20}{c}} {0 \; {\rm{si}}\; x < x_0}\\ {\displaystyle{\frac{\alpha}{x_0}\left(\frac{x_0}{x}\right)^{\alpha + 1}\; {\rm{si}}\; x \geqslant x_0}} \end{array}} \right.\)
Représentation graphique pour \(α = 2\) et \(x_0 = 1\) (GeoGebra) :
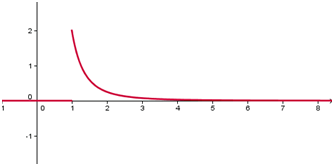
Bien sûr, la fonction n’a d’intérêt que pour \(x > x_0.\)
\(F(x)\) \(=\) \(\left\{ {\begin{array}{*{20}{c}} {0 \; {\rm{si}}\; x < x_0}\\ {\displaystyle{1 - \left(\frac{x_0}{x}\right)^{\alpha}\; {\rm{si}}\; x \geqslant x_0}} \end{array}} \right.\)
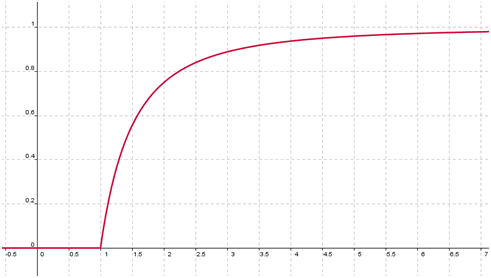
Une valeur de \(α\) proche de 2 est habituelle pour modéliser des répartitions de revenu. Comment alors interpréter la courbe ci-dessus ? Environ les trois quarts de la population ont un revenu inférieur à 2.
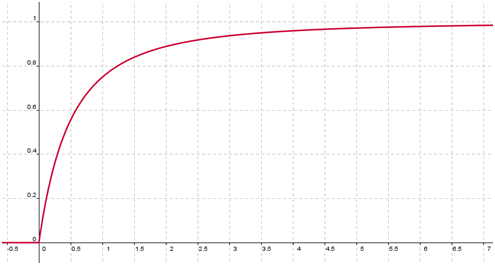
Il est souvent plus pratique d’opérer une translation. Ainsi…
\(\displaystyle{F(x) = 1 - \left(\frac{x_0}{x + x_0} \right) ^{\alpha}}\)
Pour \(α > 1,\) l’espérance est \(E(X)\) \(=\) \(\displaystyle{\frac{\alpha x_0}{\alpha - 1}}.\)
Pour \(α > 2,\) la variance est \({\rm{Var}}(X)\) \(=\) \(\displaystyle{\frac{\alpha x_0^2}{(\alpha - 1)^2(\alpha - 2)}}\)
L’écart-type s’en déduit aisément : \(\sigma(X)\) \(=\) \(\displaystyle{\frac{x_0}{\alpha - 1} \sqrt{\frac{\alpha}{\alpha - 2}}}\)
La médiane : \(\displaystyle{{\rm{Me}} = x_0 \sqrt[\alpha]{2}}\)
Enfin, il est évident que le mode est égal à \(x_0.\)
La variable aléatoire \(Y = \ln \frac{X}{x_0}\) suit une loi exponentielle de paramètre \(- α.\)
Loi de Zipf
Il existe une version discrète de cette loi de probabilité. C’est la loi de Zipf (ou Zeta).
