Problèmes de probabilités (niveau première)
Cette page d’exercices est destinée aux élèves de première générale. Il s’agit de deux problèmes qui concernent les probabilités mais aussi des notions abordées dans d’autres chapitres.
Problème 1
Une animation doit être organisée par le comité des fêtes de Probaville. Chaque joueur achètera un double coupon qui lui permettra de participer à deux loteries.
La première loterie doit comporter un billet gagnant pour \(n\) billets perdants et la seconde doit comporter deux billets gagnants pour \(n\) perdants.
Construire un arbre pondéré décrivant la situation puis déterminer \(n\) de façon que la probabilité pour un joueur de gagner les deux fois soit égale à \(\frac{1}{3}.\)
Problème 2
Les festivités continuent à Probaville. Un concours de fléchettes lancées les yeux bandés est organisé (écartez-vous, il y a des risques). La cible ressemble à ceci :
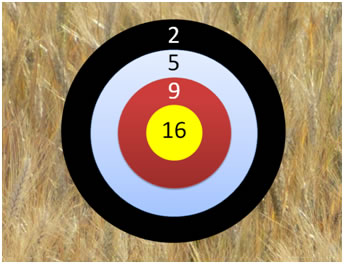
On admettra que les rayons des cercles qui structurent la cible mesurent 1, 2, 3 et 4. On admettra également que la probabilité de rater la cible est d’un risque sur cinq et que celle d’atteindre une zone est strictement proportionnelle à la surface de celle-ci. Soit \(X\) la variable aléatoire qui associe le nombre de points à un lancer. Déterminer la loi de probabilité de \(X,\) son espérance et son écart-type.
Corrigé 1
Notons \(P\) l’évènement « Billet perdant » et \(G\) l’évènement « Billet gagnant ». L’arbre apparaît ainsi (le premier embranchement correspond à la première loterie et le second indique la seconde loterie) :
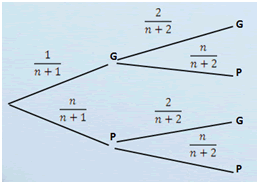
\(n\) doit vérifier l’égalité suivante :
\(P(G_1 \cap G_2)\) \(=\) \(\frac{1}{n+1} \times \frac{2}{n+2}\) \(=\) \(\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{(n+1)(n+2)}\) \(=\) \(\frac{1}{3}\)
\(\Leftrightarrow \frac{2}{n^2 + 3n + 2}\) \(=\) \(\frac{1}{3}\)
Faisons un produit en croix : \(6 = n^2 + 3n + 2,\) ce qui revient à résoudre l’équation \(n^2 + 3n - 4 = 0.\)
Nous avons à présent un banal exercice sur le second degré à résoudre. Le discriminant \(Δ\) est égal à \(9 + 16 = 25,\) soit \(5^2.\) Comme il est positif, l’équation admet deux solutions :
\(n_1 = \frac{-3-5}{2} = -4\)
Cette solution étant négative, elle ne peut convenir au problème posé.
\(n_2 = \frac{-3+5}{2} = 1\)
Voilà qui est mieux. Il faut donc que \(n\) soit égal à 1. Ainsi, le billet de la première loterie a une chance sur deux d’être gagnant et celui de la seconde loterie a deux chances sur trois de l’être.
Corrigé 2
Pour résoudre ce problème, il faut se remémorer la formule de l’aire d’un disque de rayon \(r\) : c'est \(π r^2.\) Commençons par le disque jaune : son aire vaut \(π.\) L’unité de mesure n’est pas précisée dans l’énoncé car elle n’a aucune importance dans le cadre de notre problème. Passons ensuite au disque rouge : \(4π.\) Mais il faut lui enlever l’aire du cercle jaune. Donc, zone rouge \(= 3π.\) Et ainsi de suite. Zone bleue \(= 5π\) et zone noire \(= 7π\) (suite arithmétique de raison \(2π\)).

Pour calculer les proportions de chaque zone, il est inutile de conserver les facteurs π qui se neutralisent. Par exemple, la zone jaune représente, en proportion du total de la cible…
\(\displaystyle{\frac{\pi}{\pi + 3\pi + 5\pi + 7\pi}}\) \(=\) \(\displaystyle{\frac{\pi}{16\pi}}\) \(=\) \(\displaystyle{\frac{1}{16}}\)
De même, la zone rouge représente \(\frac{3}{16},\) la bleue \(\frac{5}{16}\) et la noire \(\frac{7}{16}\) de la cible.
Mais ces proportions ne sont pas égales aux probabilités cherchées puisque la fléchette peut partir dans le décor une fois sur cinq. En d’autres termes, la probabilité de rater la cible est de 0,2 et celle de l’atteindre est donc de 0,8.
Par conséquent, les proportions de chaque zone de la cible doivent être multipliées par 0,8.
Et c’est reparti.
- Zone jaune : \(\displaystyle{\frac{1}{16} × 0,8 = 0,05}.\)
- Zone rouge : \(\displaystyle{\frac{3}{16} × 0,8 = 0,15}.\)
- Zone bleue : \(\displaystyle{\frac{5}{16} × 0,8 = 0,25}.\)
- Zone noire : \(\displaystyle{\frac{7}{16} × 0,8 = 0,35}.\)
D’où la loi de probabilité suivante :
| \(x_i\) | 0 | 2 | 5 | 9 | 16 |
| \(P(X=x_i)\) | 0,20 | 0,05 | 0,15 | 0,25 | 0,35 |
L’espérance s'établit à \((0 × 0,2)\) \(+\) \((2 × 0,05)\) \(+\) \((5 × 0,15)\) \(+\) \((9 × 0,25)\) \(+\) \((16 × 0,35)\) \(=\) \(8,7\)
On peut espérer obtenir 8,7 points en moyenne par lancer.
Avec la calculatrice, on trouve que l’écart-type est d’environ 6,17.
