Exercice d'initiation aux statistiques descriptives
Voici un exercice simple de statistiques descriptives. Le niveau de difficulté est celui de la classe de seconde. Il montre comment on peut exploiter une série statistique brute pour en extraire des informations. La fonction statistique de la calculatrice ne sera pas utilisée pour bien détailler la façon dont sont obtenus les différents paramètres.
Énoncé
Des concessionnaires automobiles relèvent pendant deux mois, soit quarante-cinq jours ouvrés, le nombre de véhicules vendus quotidiennement. Ils obtiennent 2 ; 0 ; 1 ; 0 ; 3 ; 1 ; 0 ; 2 ; 1 ; 4 ; 3 ; 1 ; 2 ; 0 ; 4 ; 2 ; 3 ; 1 ; 0 ; 2 ; 2 ; 2 ; 5 ; 1 ; 2 ; 0 ; 0 ; 1 ; 2 ; 4 ; 1 ; 2 ; 3 ; 0 ; 1 ; 2 ; 2 ; 1 ; 4 ; 5 ; 3 ; 1 ; 2 ; 0 ; 2.
Présenter ces chiffres sous forme de tableau en indiquant les fréquences et les fréquences cumulées. Déterminer la moyenne, la médiane, les quartiles, l’étendue et représenter le diagramme en boîte (Note : il n'est pas rare que les élèves de seconde découvrent le diagramme en boîte mais celui-ci ne figure pas expressément au programme).
Calculer la variance (au cas où vous connaissez cette notion qui n'apparaît pas au programme) et l'écart-type.

Corrigé détaillé
Le caractère qui nous intéresse est le nombre de véhicules vendus par jour et l’effectif est le nombre de jours. Cette distinction est fondamentale et une bonne partie des erreurs commises par les lycéens vient de la confusion entre le caractère et l’effectif.
Commençons par le travail le plus ennuyeux : il faut compter combien il y a de 0, de 1, etc. Ceci permet d’établir un tableau trié par ordre croissant du caractère étudié :
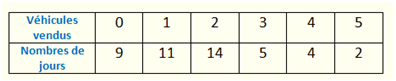
Par prudence, vérifions que \(9 + 11 + 14 + 5 + 4 + 2\) \(=\) \(45\)
D’ores et déjà, nous pouvons calculer la moyenne. Celle-ci est bien sûr pondérée par les effectifs :
\(\overline{x}\) \(=\) \(\frac{9 \times 0 + 11 \times 1 + 14 \times 2 + 5 \times 3 + 4 \times 4 + 2 \times 5}{45}\) \(\approx\) \(1,78\)
Chaque effectif (nombre de jours) est divisé par l’effectif total, c’est-à-dire 45, pour obtenir la fréquence.
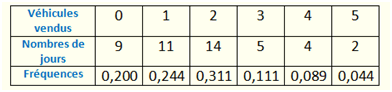
Là aussi, nous vérifions la somme des fréquences. Elle doit être égale à 1, éventuellement un peu plus ou un peu moins à cause des arrondis. Pour obtenir les fréquences cumulées, on ajoute les fréquences entre elles.
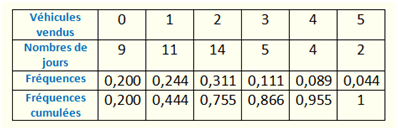
En raison des arrondis, nous nous permettons de tricher un peu pour faire apparaître 1 (car 0,999 ferait mauvais effet !).
Ce tableau permet de trouver la médiane, c’est-à-dire le nombre de véhicules vendus pour une fréquence cumulée de 0,5. Il ne faut pas dire que « c’est entre 1 et 2 » mais bien que la médiane est de 2 véhicules par jour. En effet, si l’on trie tous les jours en ordre croissant de véhicules vendus, on constate qu’il a été vendu deux véhicules le jour du milieu (qui est le 23e).
De même le premier quartile (\(Q1)\) est 1 et le troisième quartile \((Q3)\) est 2. Ici, la médiane est donc égale au troisième quartile. L’écart interquartile s’établit à 1. Remarque : \(Q\)3 est égal à 2 lorsqu'on utilise cette technique qui est celle du programme de l'Éducation Nationale en France. En fait, \(Q3\) tombe entre 2 et 3 et si vous utilisez la fonction statistique d'une calculatrice ou un logiciel, vous obtiendrez \(Q3 = 2,5.\)
L’étendue est donc de \(5 - 0 = 5.\)

Le diagramme en boîte est représenté ci-dessous. Comme la médiane et \(Q3\) sont confondus, j’ai indiqué la médiane par un trait rouge.
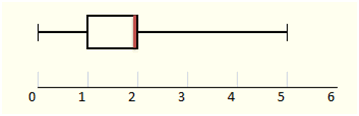
La dispersion est assez faible (écart interquartile de 1 seulement). Cette distribution est typique des caractères qui prennent de petites valeurs entières avec une impossibilité de s’étendre à gauche (on ne vend pas un nombre négatif de véhicules). La moyenne et la médiane sont proches mais compte tenu du faible nombre de valeurs que peut prendre le caractère observé, la médiane n’est pas un indicateur très pertinent sur cet exemple.
La variance est la moyenne pondérée des carrés des différences entre les valeurs du caractère observé et sa valeur moyenne (pas facile à expliquer en une phrase !). L’écart-type est la racine carrée de la variance.
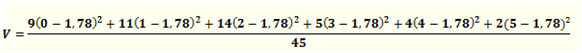
En principe, sur une copie, on indique la façon de calculer la variance (comme ci-dessus) mais on utilise la fonction statistique de la calculatrice pour trouver directement le résultat. Comme nous ne manquons pas de courage, calculons tout de même la variance « à l’ancienne »…
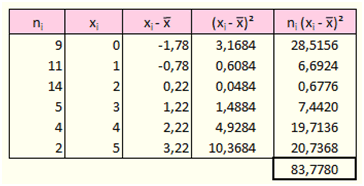
D’où \(V = \frac{83,778}{45} = 1,8617\)
Il s'ensuit que \(σ = 1,3645.\)
