Une suite avec logarithme de base a

Exercice avec log₃

Voici un exercice de suite qui peut être réalisé en classe de terminale générale, bien que le logarithme de base \(a\) ne soit pas au programme. En effet, le rappel théorique ci-dessous suffit pour vous lancer à l’assaut de l’exercice.

Rappel

Enfin... rappel ou préambule parce que vous n'êtes pas censé savoir ce qui suit !

Le logarithme népérien est de base \(e\) mais il existe une infinité d’autres logarithmes, notamment les décimaux. Dans cet exercice, nous trouverez un logarithme de base 3. Quel est le lien entre un logarithme népérien et un logarithme de base \(a\) ? Réponse avec la formule suivante :

\(\log_a(x) = \frac{\ln x}{\ln a}\)

Remarquez au passage la façon d’écrire un logarithme non népérien. Ça y est, vous savez tout.

Énoncé

Soit la suite \((u_n)\) définie par \(u_0 = 1\) et \(u_{n+1} = \frac{1}{2}u_n - \frac{3}{2}\) avec \(n \in \mathbb{N}.\)

On considère la suite \((v_n)\) telle que \(v_n = u_n + 3.\)

1. Montrer que la suite \((v_n)\) est géométrique. Donner l’expression de \(v_n\) puis celle de \(u_n\) en fonction de \(n.\)


2. Calculer \(S_n = v_0 + v_1 + … + v_n\) puis \(\Sigma_n = u_0 + u_1 + … + u_n.\)


3. Démontrer que la suite \((w_n)\) définie par \(w_n = \log_3 (v_n)\) est arithmétique. Déterminer sa raison et son premier terme.

Corrigé question 1

Nous avons \(u_0 =1\) et \(u_{n+1} = \frac{u_n - 3}{2}\)

Le premier terme de \((v_n)\) est \(v_0 = u_0 + 3\) soit \(1 + 3 = 4.\)

\(\displaystyle {\frac{v_{n+1}}{v_n} = \frac{\frac{u_n - 3}{2} + 3}{u_n + 3}}\)
\(\displaystyle {\Leftrightarrow \frac{v_{n+1}}{v_n} = \frac{\frac{u_n - 3}{2} + \frac{6}{2}}{u_n + 3}}\)
\(\displaystyle {\Leftrightarrow \frac{v_{n+1}}{v_n} = \frac{\frac{u_n + 3}{2}}{u_n + 3}}\)
\(\ \Leftrightarrow \frac{v_{n+1}}{v_n} = \frac{1}{2}\)

La suite \((v_n)\) est géométrique de raison \(q = \frac{1}{2}\) et de premier terme \(v_0 = 4.\)

\(v_n = v_0 \times q^n\)
\(v_n = 4 \times \frac{1}{2^n}\)
\(\Leftrightarrow v_n = \frac{1}{2^{n-2}}\)

\(u_n = v_n - 3\)
\(\Leftrightarrow u_n = \frac{1}{2^{n-2}} - 3\)

Corrigé question 2

Soit \(S_n = v_0 + v_1 + … + v_n\)

\(S_n = v_0 \times \frac{1 - q^{n+1}}{1 - q}\)
\( \displaystyle{S_n = 4 \times \frac{1 - (\frac{1}{2})^{n+1}}{\frac{1}{2}}}\)
\(\Leftrightarrow S_n = 8 \times \left(1 - (\frac{1}{2})^{n+1} \right)\)
\(\Leftrightarrow S_n = 8  -  8(\frac{1}{{2}^{n+1}})\)
\(\Leftrightarrow S_n = 8  -  \frac{2^3}{{2}^{n+1}}\)
\(\Leftrightarrow S_n = 8  -  \frac{1}{{2}^{n-2}}\)

\(\Sigma_n = u_0 + u_1 + … + u_n\)

\(\Sigma_n = (v_0-3) + (v_1-3) + … + (v_n-3)\)
\(\Leftrightarrow \Sigma_n = S_n + (-3)\times(n+1)\)
\(\Leftrightarrow \Sigma_n = \left(8 - \frac{1}{2^{n-2}} \right) -3n - 3\)
\(\Leftrightarrow \Sigma_n = 5 - 3n - \frac{1}{2^{n-2}}\)

Non demandé par l'énoncé mais offert généreusement par la maison :

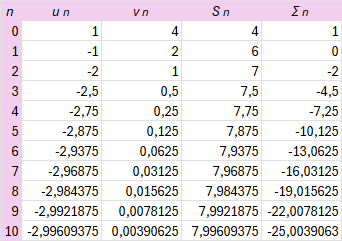
Corrigé question 3

Soit \(w_n = \log_3 (v_n)\)

Attention, ne pas recourir à la suite \((u_n).\)

\(w_{n+1} - w_n = \frac{\ln v_{n+1}}{\ln 3} - \frac{ \ln v_n}{\ln 3}\)
\(\Leftrightarrow w_{n+1} - w_n = \frac{\ln v_{n+1} - \ln v_n}{\ln 3}\)

Utilisons une propriété des logarithmes.

\(\displaystyle { w_{n+1} - w_n = \frac{ \ln \left( \frac{v_{n+1}}{v_n} \right)}{\ln 3} }\)

D’après la question 1, nous pouvons écrire…

\(\displaystyle { w_{n+1} - w_n = \frac{ \ln \left( \frac{1}{2} \right)}{\ln 3} }\)
\( w_{n+1} - w_n = -\frac{\ln 2}{ln 3} \)

La suite \((w_n)\) est arithmétique de raison \(-\frac{\ln 2}{ln 3} \) soit environ -0,631.

Son premier terme est \(w_0 = \log_3 (v_0),\) soit \(\log_3 4.\) Ce nombre s’écrit aussi \(\frac{\ln 4}{\ln 3}\) soit environ 1,262.