Aire d'un triangle et loi des sinus
La loi des sinus permet de résoudre certains problèmes de géométrie. En France, son enseignement n’est pas obligatoire dans le secondaire mais elle est mentionnée comme « approfondissement possible » dans le programme de première générale (curieusement, dans le chapitre sur le produit scalaire).
Alors approfondissons.
Aire d’un triangle
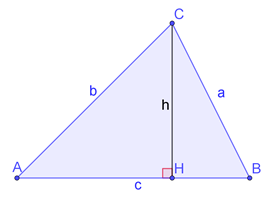
Soit un triangle \(ABC\) et soit \(\mathscr{A}\) son aire. Soit \(H\) le pied de la hauteur issue de \(C.\)
Vous le savez depuis longtemps, l’aire d’un triangle est égale à sa base que multiplie sa hauteur divisée par 2.
\(\mathscr{A} = \frac{AB × CH}{2}\)
Pour simplifier l’écriture des formules, nous nommerons \(a\) la longueur de \(BC,\) \(b\) celle de \(AC\) et \(c\) celle de \(AB.\) Et appelons \(h\) la hauteur issue de \(C.\) Donc \(\mathscr{A} = \frac{ch}{2}.\)
Mais on peut se passer de la hauteur. L’aire se détermine aussi à partir du sinus d’un angle et des deux côtés qui le forment.
\(\mathscr{A} = \frac{1}{2} bc × \sin \widehat A\)
Démontrons-le.
\(ACH\) est un triangle rectangle en \(H.\)
Rappelons que dans un triangle rectangle le sinus d’un angle est le rapport entre le côté opposé et l’hypoténuse (voir la page sur la trigonométrie en degrés) . Donc \(\sin \widehat A = \frac{h}{b}\) et donc \(h = b \sin \widehat A.\)
Plus haut nous avons rappelé que \(\mathscr{A} = \frac{ch}{2}.\) En remplaçant \(h\) par ce que nous venons d’établir, il s’ensuit que \(\mathscr{A} = \frac{1}{2} bc × \sin \widehat A.\) Retenez-le car nous en aurons besoin dans la démonstration qui va suivre.
Loi des sinus
\(\frac{{\sin \widehat A}}{{BC}} = \frac{{\sin \widehat B}}{{AC}} = \frac{{\sin \widehat C}}{{AB}} = \frac{{2\mathscr{A}}}{{BC \times AC \times AB}}\)
Bien entendu, l’égalité fonctionne aussi avec les inverses. Comme nous étudions un triangle, les côtés ne sont pas nuls et les angles non plus.
Pour déterminer la longueur d’un côté, vous utiliserez soit la loi des sinus soit le théorème d’Al Kashi selon les données dont vous disposez.
L'aire d'un triangle déterminée par les longueurs de deux côtés et un sinus sert notamment à la démonstration de la formule de Brahmagupta.
Démonstration
Plus haut nous avons montré que \(\mathscr{A} = \frac{1}{2} bc × \sin \widehat A.\) De la même manière, nous aurions pu montrer que \(\mathscr{A} = \frac{1}{2} ac × \sin \widehat B\) ou encore \(\mathscr{A} = \frac{1}{2} ab × \sin \widehat C.\)
Comme ces trois expressions de \(\mathscr{A}\) sont égales, on en déduit la loi des sinus.
\(\frac{{\sin \widehat A}}{a} = \frac{{\sin \widehat B}}{b} = \frac{{\sin \widehat C}}{c}\)
Il nous reste un détail à régler. Savoir pourquoi ces expressions sont égales à \(\frac{{2\mathscr{A}}}{abc}.\)
Si \(\mathscr{A} = \frac{1}{2} bc × \sin \widehat A\) alors \( \sin \widehat A = \frac{2\mathscr{A}}{bc}.\)
Divisons les deux membres de l’égalité par \(a\) (qui est évidemment non nul).
\(\frac{\sin \widehat A}{a} = \frac{2\mathscr{A}}{abc}\)
Bien entendu l’inverse est vérifié puisque les angles ne sont pas nuls.
\(\frac {a}{\sin \widehat A} = \frac{abc}{2\mathscr{A}}\)
Et ceci se vérifie aussi avec \(\frac {b}{\sin \widehat B}\) et \(\frac {c}{\sin \widehat C}.\)
Exercice
Soit un triangle \(ABC.\) Par commodité, on notera encore \(AB = c,\) \(AC = b\) et \(BC = a.\)
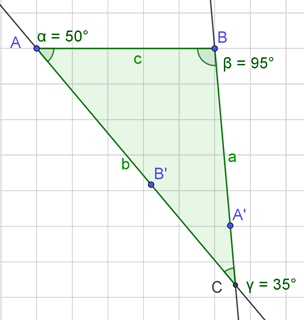
Soit \(c = 5 \) cm, \(\widehat A = 50°\) et \(\widehat C = 35°.\) Déterminer le périmètre et l’aire du triangle.
Corrigé
Commençons par le plus simple : trouver la mesure de \(\widehat B.\) Sachant que la somme des angles d’un triangle est de 180°, on en conclut que \(\widehat B = 180 - 50 - 35 = 95°.\)
Ensuite c’est la règle de trois qui entre en piste.
\(\frac{\sin 35}{5} = \frac{\sin 50}{a} = \frac{\sin 95}{b}\)
Notez que pour utiliser cette technique nous devons connaître les mesures d’un angle, du côté opposé à cet angle et deux autres informations (dont une que nous avons déduite de l’énoncé).
\(a = \frac{5\sin 50}{\sin 35}\) ce qui donne, après usage de la calculatrice et arrondi à deux décimales, 6,68 cm.
\(b = \frac{5 \sin 95}{\sin 35}\) soit 8,68 cm environ.
Le périmètre du triangle s’établit à \(5 + 6,68 + 8,68 = 20,36\) cm.
Aire : \(\frac{1}{2} × 8,68 × 5 × \sin 50\) \(= 16,62\) cm².
Il n’est pas difficile de vérifier ces résultats avec GeoGebra. Placez \(A\) et \(B\) à une distance de 5 carreaux, puis tracez les deux autres côtés du triangle à l’aide du bouton Angle de mesure donnée (GeoGebra crée alors des points \(A’\) et \(B’\)). Placez \(C\) à l’intersection de ces deux droites. Ensuite, utilisez les trois points pour tracer le triangle (bouton Polygone). Vous n’avez plus qu’à lire les mesures de ses côtés et son aire dans la fenêtre Algèbre.