Produit scalaire dans un repère de l'espace
Niveau de cette page : terminale (maths de spécialité).
Vous avez étudié le produit scalaire dans le plan en classe de première et vous avez dû remarquer que les exercices devenaient plus faciles lorsqu’ils avaient pour cadre des plans repérés. Eh bien c’est pareil dans l’espace.
Base orthonormée
Un repère orthonormé dans l’espace \((O\,;\overrightarrow i ,\overrightarrow j ,\overrightarrow k )\) est un repère dans lequel les vecteurs \( \overrightarrow i ,\) \(\overrightarrow j\) et \(\overrightarrow k \) sont deux à deux orthogonaux et leurs normes sont toutes trois égales à 1.
Pour illustrer, si vous vous trouvez dans une pièce où les murs sont droits, vous vous situez dans un repère orthogonal. À moins que vous ayez l’idée farfelue de mesurer un mur en centimètres et un autre en pouces, il est orthonormé.
Le triplet \((\overrightarrow i ,\overrightarrow j ,\overrightarrow k )\) est la base orthonormée de l’espace. Tout ceci est très simple. Il s’agit juste de ne pas confondre repère et base.

Produit scalaire
Le calcul du produit scalaire est particulièrement simple lorsqu'on dispose des coordonnées de deux vecteurs, soit respectivement \((x\,;y\,;z)\) et \((x'\,;y'\,;z').\) Nous l’obtenons par \(\overrightarrow u .\overrightarrow v\) \(= xx' + yy' + zz'.\)
Exemple d’utilisation : soit trois points de l’espace orthonormé \(A(2\, ;3\, ;-1),\) \(B(1\, ;-4\, ;0)\) et \(C(x\, ;1\, ;-3).\) Déterminons \(x\) pour que les vecteurs \(\overrightarrow {AB}\) et \(\overrightarrow {AC}\) soient orthogonaux.
Les calculs de \(\overrightarrow {AB}\) et de \(\overrightarrow {AC}\) ne posent pas de difficulté. Vous pouvez les présenter en ligne ou en colonne.
\(\overrightarrow {AB} (-1\, ;-7\, ;1)\) et \(\overrightarrow {AC} (x-2\, ;-2\, ;-2).\)
Rappelons que deux vecteurs non nuls sont orthogonaux si et seulement si leur produit scalaire est nul.
\(-(x - 2) - 7× (-2) - 2 = 0\)
\(⇔ -x + 2 + 14 - 2 = 0\)
\(⇔ x = 14\)
Visualisons ceci avec GeoGebra. Il faut opter pour Graphique 3D dans Affichage.
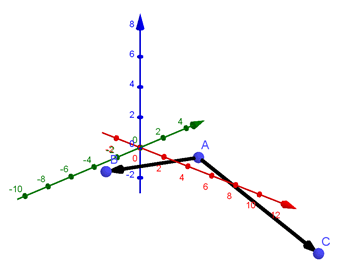
On peut tournoyer dans le graphique comme si l’on était dans un avion pour varier les points de vue.
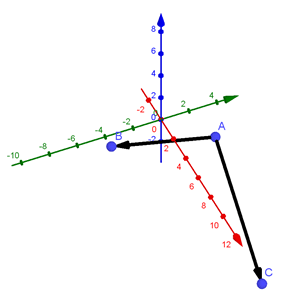
Ici, l’orthogonalité apparaît mieux…
Norme
Soit le vecteur \(\overrightarrow u (x\, ;y\, ;z).\) Employons la formule du produit scalaire. Il est clair que \(\overrightarrow u . \overrightarrow u = x^2 + y^2 + z^2.\)
Par conséquent, \(|\overrightarrow u | = \sqrt{x^2 + y^2 + z^2}\)
Distance et milieu
Vous l’avez certainement deviné à partir de ce qui précède (ou de vos souvenirs de seconde).
Situons-nous dans un repère orthonormé.
\(AB = \sqrt{(x_B - x_A)^2 + (y_B - y_A)^2 + (z_B - z_A)^2}\)
Et le milieu de \([AB]\) a pour coordonnées \(\left(\frac{x_A + x_B}{2}\, ; \frac{y_A + y_B}{2}\, ;\frac{z_A + z_B}{2}\right)\)
Exemple.
Soit les points \(A(2\, ;-3\, ;4),\) \(B(7\, ;4\, ;-1),\) \(C(5\, ;2\, ;2)\) et \(D(0\, ;-5,\ ;7).\)
Le quadrilatère \(ABCD\) est-il un parallélogramme ? Si oui est-ce un rectangle ?
Réfléchissez.
C’est bon ? Alors corrigé.
Un parallélogramme est un quadrilatère dont les diagonales ont le même milieu.
Après calcul, il s’avère que c’est le cas. Les coordonnées du milieu sont \((5,5\, ;-0,5\, ;3).\) Nous aurions aussi pu calculer les longueurs des côtés mais cela aurait été un peu plus long.
Un rectangle est un parallélogramme dont les diagonales se croisent à angle droit. Autrement dit, \(ABCD\) est un rectangle si \(\overrightarrow {AC}\) et \(\overrightarrow {BD}\) sont orthogonaux.
\(\overrightarrow {AC} (3\, ;5\, ;-2)\) et \(\overrightarrow {BD} (-7\, ;-9\, ;8)\)
\(\overrightarrow {AC} . \overrightarrow {BD} = -21 – 45 – 16 = -82.\)
Comme \(\overrightarrow {AC} . \overrightarrow {BD} ≠ 0\) les vecteurs ne sont pas orthogonaux. Donc \((AC)\) et \((BD)\) ne se croisent pas à angle droit et par conséquent \(ABCD\) n’est pas un rectangle, ce que nous regrettons tous.

s