Exercices et démonstration sur la convexité
Cette page vous invite à réfléchir sur deux exercices traitant de la convexité des fonctions et à une démonstration, de niveau terminale (spécialité maths). Mais d'abord, un petit rappel.

Inégalité des tangentes
Soit \(f\) une fonction deux fois dérivable sur un intervalle \(I .\) Soit \(x_0\) un réel appartenant à \(I.\)
Si \(f'' \geqslant 0\) sur \(I,\) alors \(f(x_0) \geqslant f(x_0) + f'(x_0)(x – x_0)\)
Et inversement si \(f'' \leqslant 0.\)
Exercice 1 : lecture graphique
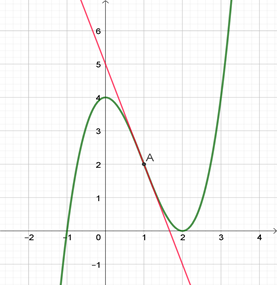
Ci-dessous figure la courbe représentative d'une fonction \(g\) définie sur \(\mathbb{R}\) et sa tangente au point d'abscisse 1. Que peut-on dire sur la convexité de \(f\) ?
Corrigé
Exercice très facile. La tangente en \(A\) est au-dessus de la courbe pour \(x < 1\) et au-dessous pour \(x > 1.\) Le point \(A\) est donc un point d'inflexion. \(f\) est concave sur \([- ∞\, ; 1]\) et convexe sur \([1\, ; + ∞[.\)
Exercice 2 : inégalité des tangentes
Montrer avec l'inégalité des tangentes que, sur \(\mathbb{R}^*_+\) nous vérifions toujours l'inégalité \(\frac{1}{x} \geqslant -x+2.\)
Corrigé
Nous devons d'abord trouver un éventuel point de tangence.
\(\frac{1}{x} = -x + 2\)
\(\Leftrightarrow 1 = -x^2 + 2x\)
\(\Leftrightarrow x^2 - 2x + 1 =0\)
\(\Leftrightarrow (x - 1)^2 = 0\)
\(\Leftrightarrow x = 1\)
Visualisation :
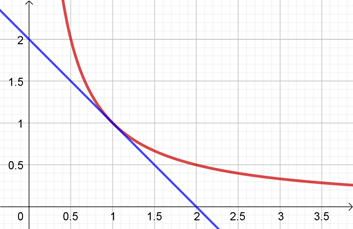
Déterminons l'équation de la tangente en 1 de la fonction inverse.
\(f'(1) = -\frac{1}{1^2} = -1\)
\(f(1) = \frac{1}{1} = 1\)
\(y = 1 - (x - 1) = -x + 2\)
Nous savons que sur \(\mathbb{R}^*_+\) la fonction inverse est convexe, donc les tangentes se situent au-dessous de sa courbe représentative.
Comme la droite d'équation \(y = -x + 2\) est tangente à la courbe, alors elle se situe au-dessous.
Donc \(\frac{1}{x} \geqslant -x+2\) pour tout \(x > 0.\)
Démonstration de l'inégalité des tangentes
C'est une démonstration qui fait partie du programme de terminale : si \(f''\) est positive, alors la courbe représentative de \(f\) est au-dessus de ses tangentes.
Supposons que \(f''\) est positive sur un intervalle \(I.\)
Si la courbe représentative de \(f\) est au-dessus de sa tangente pour tout point d'abscisse \(x_0\) de \(I,\) on doit vérifier :
\(f(x) \geqslant f(x_0) + f'(x_0)(x - x_0)\)
Soit une fonction \(g\) définie comme suit :
\(g(x) = f(x) - f(x_0) - f'(x_0)(x - x_0)\)
\(g\) est définie et dérivable sur \(I\) puisque c'est la somme de deux fonctions dérivables.
\(g'(x) = f'(x) - f'(x_0)\)
Partant de l'hypothèse que \(f''\) est positive sur \(I,\) nous en déduisons que \(f'\) est croissante. Donc \(g'(x) = 0\) pour \(x = x_0,\) et donc négative pour \(x < x_0\) et positive pour \(x > x_0.\)
Dressons le tableau de variation de \(g(x)\) (ci-dessous réalisé avec Sine qua non, très bon logiciel gratuit pour produire des tableaux de variations).
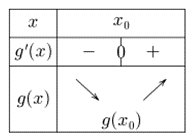
Déterminons à présent la valeur de \(g(x_0).\) Rien de compliqué.
\(g(x_0) = f(x_0) - f(x_0) - f'(x_0)(x_0 - x_0) = 0\)
La fonction \(g\) ayant pour minimum zéro, elle est positive.
Donc \(f(x) \geqslant f(x_0) + f'(x_0)(x - x_0)\) ce qui signifie que la courbe est au-dessus de sa tangente en \(x_0.\)
