Exercice sur loi binomiale et fluctuations d'échantillonnage
La progression de l’exercice qui suit est assez classique. Un élève de terminale doit être capable de résoudre ce type de problème qui fait intervenir la loi binomiale.
Les deux dernières questions concernent l’échantillonnage et plus précisément la détermination d’intervalles de fluctuation au seuil de \(95\%.\) Ces sujets ayant disparu des programmes du secondaire, nous ne les avons laissés que pour les internautes qui suivent des études supérieures.
Énoncé
Un philatéliste acquiert un lot très important de timbres en vrac aux sujets variés. Son fournisseur lui a assuré que le lot contenait \(5\%\) de timbres sur le thème du sport (ce sont ceux que notre collectionneur préfère).

Partie 1
Le philatéliste tire cinq timbres au hasard. Soit \(X\) la variable aléatoire égale au nombre de timbres de sport obtenus. Compte tenu de la quantité importante de timbres, on considère que la probabilité de succès reste identique après chaque tirage. Dans cette partie 1, on suppose aussi que le fournisseur dit la vérité.
- Justifier que \(X\) suit une loi binomiale et préciser ses paramètres.
- Calculer la probabilité d’obtenir un seul timbre de sport.
- Calculer la probabilité d’obtenir au moins un timbre de sport.
Partie 2
Le philatéliste pioche à présent 80 timbres. Soit \(Y\) la variable aléatoire égale au nombre de timbres de sport obtenus.
- Déterminer la loi de probabilité suivie par \(Y.\)
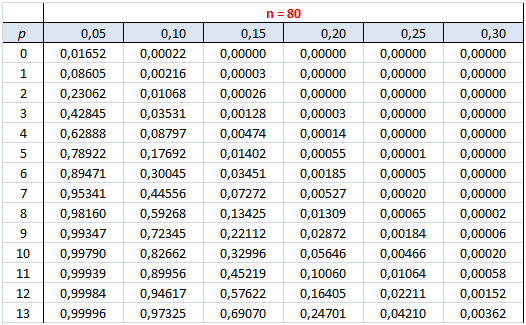
- À l’aide de la table de probabilités cumulées ci-dessous, déterminer l’intervalle de fluctuation à \(95\%\) de la fréquence correspondant à \(Y.\)
- Parmi les 80 timbres, seulement deux se rapportent au sport. Le fournisseur a-t-il menti ?
Corrigé
Partie 1
1- On considère qu’il y a répétition de cinq expériences identiques et indépendantes. Il s’agit donc d’un schéma de Bernoulli. On appelle « succès » l’évènement « le sujet du timbre est le sport ». La probabilité de succès est \(p = 0,05.\)
\(X\) suit donc la loi binomiale de paramètres 5 et 0,05 notée \(\mathscr{B}(5\,;0,05)\)
2- Obtenir un seul timbre ? La façon de répondre à cette question dépend de votre filière ! Si vous êtes en terminale générale, vous utiliserez la formule et si vous êtes en terminale technologique, vous utiliserez un tableur !
Filière générale :
\(P(X = 1)\) \(=\) \({\left( {\begin{array}{*{20}{c}}
5\\
1
\end{array}} \right)} \times 0,05 \times (1 - 0,05)^4\) \(\approx\) \(0,2036\)
Pour réaliser les calculs de loi binomiale avec une calculatrice, voir la loi binomiale à la calculatrice.
Filière technologique :
Le coefficient binomial se détermine avec le triangle de Pascal ou avec un arbre pondéré. Ci-dessous figure le triangle de Pascal.
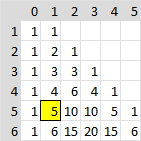
Nous n'avons pas tracé l'arbre pondéré. Il aurait montré cinq chemins comprenant un succès (probabilité de 0,05) et quatre échecs (probabilité de 0,95), ce qui permet de calculer une probabilité d'environ 0,2036.
Il peut être intéressant de répondre à cette question grâce à un tableur. Taper =LOI.BINOMIALE(1;5;0,05 ;0) dans une cellule de la feuille de calcul. On obtient 0,2036. Rappelons que le premier nombre de la formule est \(k,\) soit le nombre de succès recherché (donc 1), le deuxième paramètre est \(n\) (donc 5), le troisième est \(p\) (0,05) et le quatrième précise le souhait d’obtenir des probabilités cumulées (1) ou non cumulées (0).
3- Plutôt que calculer la probabilité d’avoir 1, puis 2 puis 3 puis 4 puis 5 timbres de sport et d’additionner tout celà, il est préférable de calculer la probabilité de n’obtenir aucun timbre de sport et de retenir la probabilité contraire. Si l’on procède comme ci-dessus, on obtient \(P (X = 0) = 0,7738.\) Donc, la probabilité d’obtenir au moins un timbre de sport s’établit à \(1 - 0,7738\) \(=\) \(0,2262\) (il est logique que cette probabilité soit un peu supérieure à \(P(X = 1)).\)
Partie 2
1- On considère qu’il y a répétition de 80 expériences identiques et indépendantes. Il s’agit là aussi d’un schéma de Bernoulli. On appelle « succès » l’évènement « le sujet du timbre est le sport ». La probabilité de succès est \(p = 0,05.\)
\(Y\) suit donc la loi binomiale de paramètres 80 et 0,05 notée \(\mathscr{B}(80\,;0,05)\)
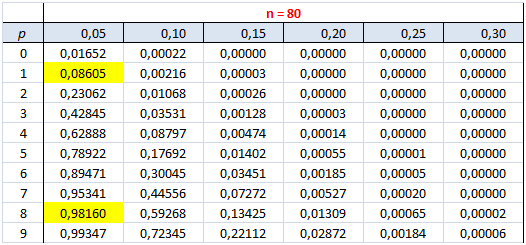
2- L’intervalle de fluctuation étant de \(95\%,\) il faut rejeter les \(2,5\%\) qui sont en-deçà et les \(2,5\%\) qui sont au-delà. En s’aidant de la table des probabilités cumulées pour \(n = 80,\) il faut s’intéresser à la colonne \(p = 0,05\) et repérer les probabilités juste au-dessus de 0,025 et de 0,975. L’espérance est bien de quatre timbres de sport (soit \(np = 80 × 0,05 = 4\)) mais, considérant les fluctuations d’échantillonnage, on admet (avec une probabilité de 0,95 d’avoir raison) qu’un échantillon comportant 1 à 8 timbres de sport ne contredit pas l’hypothèse que \(p = 0,05.\)
3- Le philatéliste s’attendait sans doute à piocher quatre timbres de sport et il n’en a obtenu que deux. Mais compte tenu des résultats précédents, il ne considère pas que le fournisseur soit un fieffé menteur.
Autres exercices
Vous pouvez poursuivre votre entraînement avec des exercices sur les paramètres de la loi binomiale.
