Loi binomiale : démonstration et table
Bienvenue sur cette présentation de la loi binomiale spécialement rédigée pour les élèves de terminale générale. Si vous êtes en terminale technologique, dirigez-vous plutôt vers la page d’initiation à la loi binomiale et si vous êtes étudiant, vers celle qui présente la loi binomiale de façon différente…
Présentation
La loi binomiale est une loi de probabilité discrète. Que modélise-t-elle ?
Un schéma de Bernoulli est répété \(n\) fois de façon identique et indépendante. La probabilité d’un succès est \(p.\) C’est cette situation que modélise la loi binomiale, qui s’appuie sur ces deux paramètres \(n\) et \(p.\)
Elle est notée \(\mathscr{B}(n\, ;p).\) Par exemple, si la probabilité de succès s'établit à 0,4 et que le nombre de tirages aléatoires identiques et indépendants est de 150, on dit que la variable aléatoire \(X\) qui dénombre les succès suit la loi \(\mathscr{B}(150\, ;0,4).\)
Soit \(k\) un nombre de succès compris entre 0 et \(n.\) La probabilité de \(X\) prenne la valeur \(k\) est donnée par la formule suivante :
\(P(X = k) = \left( {\begin{array}{*{20}{c}}
n\\
k
\end{array}} \right){p^k}{(1 - p)^{n - k}}\)
Le premier facteur est le coefficient binomial.
L’espérance de cette loi est \(E(X)= np\) (démontré en page de propriétés de l'espérance).
La variance est \(V(X) = np(1 - p).\) Par conséquent, l’écart-type est \(σ(X) = \sqrt{np(1 - p)}.\) La démonstration est en page de variables aléatoires indépendantes.
Exemple
Chaque jour, Doug photographie les oiseaux des Antilles. La probabilité de voir un colibri au cours d’une sortie est de 0,8. Durant un séjour au cours duquel il effectue 30 sorties, quelle est la probabilité qu’il voie des colibris au cours de 20 sorties exactement ?
\(P(X = 20) = \left( {\begin{array}{*{20}{c}}
{30}\\
{20}
\end{array}} \right) \times {0,8^{20}} \times {0,2^{10}} \approx 0,03547\)

En général, un problème n’est pas de connaître la probabilité pour une seule valeur de \(k\) mais un cumul pour toutes valeurs inférieures ou supérieures à \(k,\) ou pour toutes les valeurs comprises entre \(k\) et \(k’.\)
Démonstration
Soit la loi \(\mathscr{B}(n\, ;p).\) L’évènement « succès » est noté \(S\) et son évènement contraire \(\overline S.\) La probabilité de \(\overline S\) est donc \(1 - p.\)
L’évènement « les \(n\) tirages sont des succès » peut s’écrire \(S ∩ S ∩ S … ∩ S\) (\(n\) fois) et la probabilité que \(X\) prenne la valeur \(n\) est \(P(X = n) = p^n\) puisque les évènements sont indépendants.
Soit \(0 \leqslant k \leqslant n.\) L’évènement « \(k\) succès sur \(n\) » implique \(n - k\) échecs.
Considérons l’évènement \(S ∩ S…\) (\(k\) fois) \(∩ \overline S ∩ \overline S\) (\(n - k\) fois).
La probabilité de cet évènement est donc \(p^k(1-p)^{n-k}\) puisque, rappelons-le, les évènements sont indépendants.
Toutefois, l’ordre d’apparition des évènements peut être différent. L’évènement \(\overline S ∩ \overline S\) (\(n - k\) fois) \(∩ S ∩ S…\) (\(k\) fois) a la même probabilité de survenir.
Il s’agit donc de déterminer combien d’évènements sont constitués de \(k\) succès et de \(n - k\) échecs.
C'est une question de dénombrement. Comme l’ordre n’a pas d'importance, nous devons calculer une combinaison de \(k\) pris parmi \(n.\)
Cette combinaison prend la forme d'un coefficient binomial. Dans un arbre pondéré, c'est le nombre de branches qui comprennent \(k\) succès. Une illustration figure en page de succession d’évènements indépendants.
Des outils
Pour vous faciliter la vie, ce site vous propose des modes d’emploi : loi binomiale avec calculatrice TI et loi binomiale avec Excel.
Lors des âges obscurs qui ont précédé l’ère de l’informatique, les élèves disposaient de tables imprimées avec les valeurs prises par la loi binomiale. Avec un tableur, il n’est pas difficile de les ressusciter mais elles deviennent vite gigantesques si elles prennent toutes les valeurs de \(n,\) de 2 à plusieurs centaines, et si les probabilités \(p\) sont décomposées avec un pas relativement fin (au centième, par exemple). On les présente en cumulé, c’est-à-dire pour \(P(X \leqslant x).\)
Si vous souhaitez vous perfectionner avec Excel, vous pouvez construire vos tables sur-mesure. Ci-dessous, une table a été réalisée pour \(n = 30.\) Les probabilités sont celles des cumuls. Cinq valeurs de \(p\) sont indiquées, arrondies à \(10^{-5}\) près.
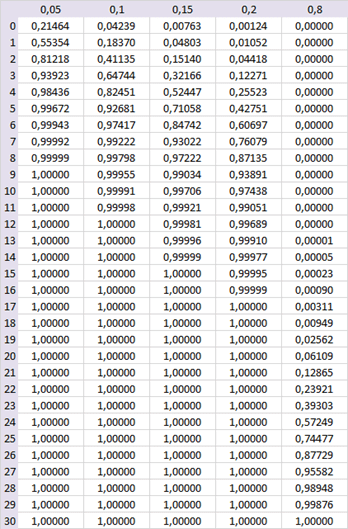
La probabilité de 0,8 a été intégrée à cette table pour faire le lien avec l’exemple vu plus haut. Dans celui-ci, nous ne cherchions pas un cumul mais la probabilité pour \(k = 20.\) Nous avions obtenu 0,03547. Pour la retrouver, situez-vous dans la dernière colonne et faites la soustraction \(P(X \leqslant 20) - P(X \leqslant 19)\) soit \(0,06109 - 0,02562\) ce qui donne bien 0,03547.
Exercices
Vous pouvez vous rendre en page d’exercices sur paramètres de la loi binomiale et d’exercice sur la loi binomiale et fluctuation d’échantillonnage (si vous n’avez pas étudié les fluctuations d’échantillonnage, arrêtez-vous avant la dernière question).
