Exercices sur la loi binomiale
Deux sympathiques exercices pour s’entraîner sur les paramètres de la loi binomiale avec en prime les corrections, voici ce qui vous attend si vous prolongez la lecture de cette page. Ils sont dans l’esprit du programme de terminale générale (maths de spécialité) dans la mesure où ils font intervenir des connaissances mathématiques extérieures aux probabilités.
Rappels préalables
La loi de probabilité de la variable aléatoire associée à une expérience aléatoire qui suit un schéma de Bernoulli est la loi binomiale. Ses deux paramètres sont le nombre \(n\) de répétitions et la probabilité de succès \(p.\)
L’espérance de cette loi est \(np.\)
Sa variance est \(npq\) avec \(q = 1 - p.\)
Exercice 1
Une variable aléatoire suit une loi binomiale \(\mathscr{B}(n\,;p).\) Est-il possible que son espérance soit égale à 5 et son écart-type à 0,5 ?
Exercice 2
Déterminez pour quelle valeur de \(p\) la variance d’une loi binomiale \(\mathscr{B}(n\,;p)\) est maximale, et ceci quelle que soit la valeur de \(n.\) Illustrez-le graphiquement pour \(n = 10.\)
Corrigé 1
Les conditions de l'énoncé seront réunies s’il existe une loi binomiale dont les paramètres \(n\) et \(p\) existent, c’est-à-dire si \(n\) est un entier naturel et si \(p\) est compris entre 0 et 1.
Nous disposons de deux informations et nous devons déterminer deux paramètres. Voici qui nous oriente naturellement vers un système de deux équations à deux inconnues.
Comme vous le savez, l’écart-type n’est autre que la racine carrée de la variance. Donc cette dernière est égale à \(0,5^2 = 0,25.\)
Posons le système.
\(\left\{ {\begin{array}{*{20}{c}} {np = 5}\\ {np(1 - p) = 0,25} \end{array}} \right.\)
À partir de là, plusieurs chemins permettent de le résoudre. Votre aisance en maths s’exprimera par le choix du plus pratique.
La substitution du produit \(np\) dans la seconde équation est certainement une bonne idée :
\(5(1 - p) = 0,25\)
\(⇔ 5 - 5p = 0,25\)
\(⇔ 5p = 4,75\)
\(⇔ p = 95\)
Remplaçons \(p\) dans la première équation.
\(0,95n = 5\)
\(⇔ n \approx 5,26\)
Nous avons bien \(0 < p < 1\) mais \(n\) n’est pas un entier.
Par conséquent, aucune loi binomiale ne peut avoir pour espérance 5 et pour écart-type 0,5.
Corrigé 2
Vous savez qu’une fonction admet un maximum lorsque sa dérivée est nulle.
Ici, la variable est \(p.\) Soit \(f\) la fonction définie sur \([0\, ; 1]\) dont l’expression est \(f(p) = np(1 - p)\)
Développons : \(f(p) = np - np^2\)
Il s’agit d’une fonction polynomiale du second degré, c’est-à-dire de type \(ax^2 + bx + c\) avec \(a = -n,\) \(b = n\) et \(c = 0.\) Comme \(a < 0,\) la fonction admet bien un maximum.
Celui-ci est atteint là où la dérivée \(f’\) s’annule.
Dériver une fonction du second degré au milieu d’un exercice, c’est un peu faire une pause. En l’occurrence : \(f’(p) = n - 2np.\)
Il faut factoriser cette expression. Nous obtenons \(f’(p) = n(1 - 2p).\)
Étape suivante : \(n(1 - 2p) = 0\)
Un produit de facteurs est nul si l’un des facteurs est nul (programme de troisième). Or, \(n\) est un entier strictement positif. Il faut donc résoudre l’équation :
\(1 - 2p = 0\)
\(⇔ p = 0,5\)
Quel que soit \(n,\) la variance d’une loi binomiale \(\mathscr{B}(n\,;p)\) est maximale lorsque \(p = 0,5.\)
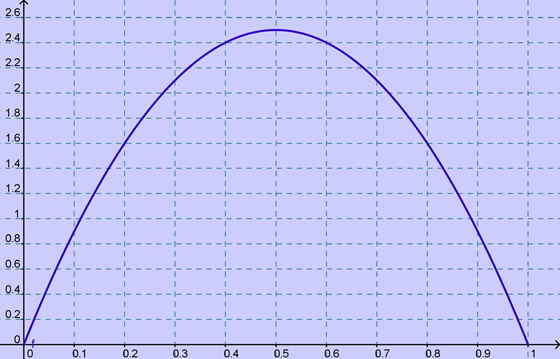
Si par exemple \(n = 10,\) alors \(f(0,5)\) \(=\) \(10 × 0,5 × (1 - 0,5)\) \(=\) \(2,5.\) La variance de la loi binomiale \(\mathscr{B}(10\,;p)\) est maximale pour \(p 0,5\) et vaut alors 2,5.
Illustration. L’axe des ordonnées indique la valeur prise par la variance. Si vous tracez la courbe avec Geogebra comme ci-dessous, entrez Fonction[10x – 10x²,0,1] pour restreindre le tracé à l’intervalle \([0 \,; 1].\)
Autre exercice
Voir la page d'exercice sur la loi binomiale.
