Une comparaison de suites

Suites au bac technologique

Cette page reprend l’extrait d’une épreuve du bac STMG, en l’occurrence celle des centres étrangers de juin 2016. Au cours de cette périlleuse mission, Il est notamment demandé de comparer deux suites (un exercice d'ailleurs assez fréquent). Ce qui suit s’adresse donc principalement aux élèves de terminale technologique mais ceux des filières générales peuvent eux aussi s’entraîner sur ce sujet, et sans le prendre à la légère ! Si la première partie peut leur sembler simple, la deuxième est un très bon entraînement à l'utilisation de la calculatrice !

 

Exercice

    Dans cet exercice, tous les résultats seront arrondis au centime d’euro.
    Justine et Benjamin sont embauchés en 2014 dans la même entreprise.
    1. Le salaire mensuel de Justine est de 1 600 € en 2014. Son contrat d’embauche stipule que son salaire mensuel augmente chaque année de \(1\%\) jusqu’en 2024.
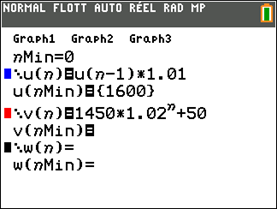
    On note \(u_0\) le salaire mensuel (en euros) de Justine en 2014 \((u_0 = 1\,600)\) et, pour tout entier \(n \leqslant 10,\) on note \(u_n\) son salaire mensuel (en euros) pour l’année \(2014 + n.\)
    a. Calculer \(u_1\) et \(u_2.\)
    b. Pour tout entier \(n\) compris entre 0 et 9, exprimer \(u_{n+1}\) en fonction de \(u_n.\)
    c. Déterminer l’expression de \(u_n\) en fonction de \(n\) pour tout entier \(n\) compris entre 0 et 10.
    d. À partir de quelle année le salaire mensuel de Justine dépassera-t-il 1 700 € ? Justifier la réponse.
    2. Le salaire mensuel hors prime de Benjamin est de 1 450 € en 2014. Son contrat d’embauche prévoit que, jusqu’en 2024, son salaire mensuel hors prime augmente chaque année de \(2\%\) et qu’il bénéficie en plus d’une prime mensuelle de 50 €.
    On note \(v_0\) le salaire mensuel (en euros) de Benjamin en 2014 \((v_0 = 1\,500)\) et, pour tout entier \(n \leqslant 10,\) on note \(v_n\) son salaire mensuel (en euros) pour l’année \(2014 + n.\)
    a. Vérifier que \(v_1 = 1\,529\) et calculer \(v_2.\)
    b. Parmi les algorithmes suivants, un seul permet de calculer le terme d’indice \(n\) de la suite \((v_n).\)
    Déterminer lequel, en expliquant la réponse.
Algorithme1 Algorithme 2 Algorithme 3

Variables
k et n sont des entiers
v est un nombre réel

Entrée
Valeur de n, n ≤ 10

Traitement
v prend la valeur 1 450
Pour k allant de 1 à n
v prend la valeur v × 1,02
v prend la valeur v + 50
FinPour

Sortie
Afficher v

Variables
k et n sont des entiers
v est un nombre réel

Entrée
Valeur de n, n ≤ 10

Traitement
v prend la valeur 1 450
Pour k allant de 1 à n
v prend la valeur v × 1,02
FinPour
v prend la valeur v + 50

Sortie
Afficher v

Variables
k et n sont des entiers
v est un nombre réel

Entrée
Valeur de n, n ≤ 10

Traitement
Pour k allant de 1 à n
v prend la valeur 1 450
v prend la valeur v × 1,02 + 50
FinPour

Sortie
Afficher v
    3. a. À partir de quelle année le salaire mensuel de Benjamin dépassera-t-il 1 700 € ?
    b. Le salaire mensuel de Benjamin peut-il dépasser celui de Justine avant 2024 ? Si oui, en quelle année ?

 

Corrigé commenté

1. a. Un taux de croissance de \(1\%\) se traduit par un coefficient multiplicateur de \(1 + (\frac{1}{100}) = 1,01.\)

Donc \(u_1 = u_0 \times 1,01,\) soit \(1\,600 \times 1,01 = 1\,616.\)

Puis \(u_2 = 1\,616 \times 1,01 = 1\,632,16.\)

Notez que l’énoncé demande de calculer les termes d’une suite et non des salaires. Vous n’avez donc pas à préciser que ce sont des montants en euros.

b. Chaque terme de la suite étant multiplié par 1,01 pour obtenir le suivant, nous avons pour tout entier \(n\) de 0 à 9 : \(u_{n+1} = 1,01u_n.\)

c. Nous avons \(u_n = 1\,600 × 1,01^n\) pour tout \(n\) compris entre 0 et 10.

Rappel de cours : l’expression du terme général d’une suite géométrique est \(u_n = u_0\,q^n.\) Nous nous situons dans ce cas-ci, bien que l’énoncé n’utilise jamais le terme « suite géométrique ».

d. Cette question nécessite la calculatrice. Si vous ne savez pas très bien l’utiliser, vous trouverez un mode d’emploi en page de suites et calculatrices (TI et Casio). C'est l’exemple d’une suite arithmétique mais le principe est le même. Il existe d’ailleurs d’autres moyens que le mode suite pour trouver le résultat.

Voici ce que l’on obtient avec une TI-83 Premium CE :

un

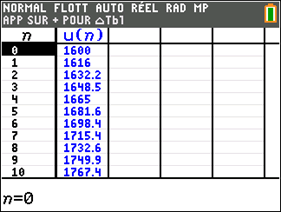
Vous remarquerez que 1 700 est dépassé pour \(n = 7.\) Comme \(u_0\) correspond à l’année 2014, \(u_7\) correspond à 2021.

C’est à partir de l’année 2021 que le salaire de Justine dépassera les 1 700 €.

2. a. Heureusement qu’une réponse est donnée car la question est piège. L’énoncé précise que \(v_0 = 1\,500\) et non 1 450. La prime est donc incluse. Mais on ne part pas directement de \(v_0\) pour trouver \(v_1.\)

En effet, le salaire de base est 1 450 que l’on multiplie chaque année par 1,02 (augmentation de \(2\%\) puis on ajoute 50.

Ainsi \(v_1 = 1\,450 × 1,02 + 50 = 1\,529.\)

De même on ne calcule pas \(v_2\) à partir de 1 529 : \(v_2 = 1\,450 × 1,02^2 + 50 = 1\,558,58.\)

b. Le premier algorithme est tombé dans le piège. Il calcule le salaire \(n + 1\) à partir du salaire \(n\) prime comprise.

Le deuxième algorithme a tout compris. L’ajout de la prime de fait pas partie de la boucle.

Le troisième algorithme est complétement dans les choux. La valeur initiale de 1 450 faisant partie de la boucle, toutes les valeurs de v seront identiques.

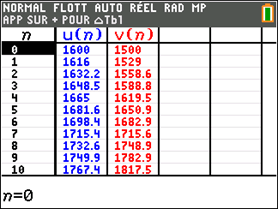
3. a. Il faut programmer l’algorithme 2 avec la calculatrice. On trouve \(v_7 = 1\,715,6.\) Donc, c’est en 2021 que le salaire de Benjamin dépassera 1 700 €.

b. Là encore c’est avec la calculatrice que l’on déterminera que le salaire de Benjamin dépassera celui de Justine en 2021. Il vous est proposé ci-dessous une formule de calcul mais vous pouvez opter pour d’autres façons d’obtenir le même résultat.

expressions de un et vn