Somme des \(n\) premiers inverses
Cette page s’adresse aux élèves de terminale, filières technologiques. Le programme de l’Éducation nationale offre la possibilité d’utiliser la somme des inverses pour illustrer la notation \(Σ\) et pour fournir un exemple d’algorithme en langage Python, rien de plus. Alors, même si nous irons un peu plus loin, ne vous attendez pas à des développements théoriques ! (si vous êtes étudiant, dirigez-vous plutôt en page de séries).
Somme des inverses
Vous connaissez la fonction inverse \(f : x ↦ \frac{1}{x}.\) Les inverses de 1, 2, 3… sont donc \(1, \frac{1}{2}, \frac{1}{3}\), etc.
Une somme s’écrit avec un sigma majuscule (lettre grecque). Au-dessous, on précise le nom de la variable (une lettre choisie arbitrairement, par exemple \(i\) ou \(k\)) et le premier rang à partir duquel on additionne, au-dessus est indiqué le dernier rang de la somme. Par exemple, la somme des entiers compris entre 2 et 7 s’écrit \(\displaystyle{\sum\limits_{k = 2}^7 k} \)
Ce symbole est particulièrement employé en statistiques.
La somme des \(n\) premiers inverses peut donc s’écrire de deux façons :
\(\sum\limits_{k = 1}^n {\frac{1}{k}}\) ou \(1 + \frac{1}{2} + \frac{1}{3} + ... + \frac{1}{n}\)

Pas de formule
On peut considérer les premiers inverses comme les termes d’une suite dont le terme général est \(u_n = \frac{1}{n}.\)
Vous connaissez la formule pour calculer la somme de termes consécutifs d’une suite arithmétique mais ce n’en est pas une. On peut le démontrer facilement à l’aide d’un contre-exemple : \(u_2 - u_1 = -\frac{1}{2}\) tandis que \(u_3 - u_2 = \frac{1}{3} - \frac{1}{2} = -\frac{1}{6}.\)
Si la suite est géométrique, vous connaissez également la formule. Mais là encore, il est facile de montrer qu'elle n’a rien de géométrique.
Hélas, le calcul direct de la somme est impossible. Il ne reste donc qu’un recours : déterminer tous les termes et les additionner. C’est moins élégant mais comme le but n’est pas de les empiler à l’infini, l’opération ne devrait pas planter votre ordinateur (sauf avec l’exercice de calcul de seuil si vous êtes imprudent). Sachez qu’à moins d’additionner les deux premiers termes (ce qui donne 1,5) le résultat présenté sous forme décimale sera une valeur approchée.
Programme
En Python, le programme peut ressembler à ceci (sans écrire de fonction) :
n = int(input('nombre de termes : '))
som = 0
for i in range(1,n+1):
u = 1/i
som = som + u
print('somme des inverses : ',som)
Si par exemple on entre 100 on obtient cet état :
![]()
Calcul de seuil
Supposons que vous vous fixez un seuil, c’est-à-dire que vous additionnez les termes jusqu’à obtenir une valeur que vous avez choisie. Vous y parviendrez avec une boucle while. Nous allons l’expérimenter avec une valeur de 5. Attention, la somme progresse très lentement et si vous prenez une valeur trop grande, vous risquez d’imposer à votre ordinateur des souffrances inutiles.
Le programme ci-dessous donne la dernière valeur avant que le seuil soit atteint. Si vous souhaitez obtenir la valeur immédiatement supérieure, il suffit de terminer par i - 1 au lieu de i - 2.
n = float(input('seuil : '))
som = 0
i = 1
while som <= n:
u = 1/i
som = som + u
i = i + 1
print("nombre d'inverses : ",i - 2)
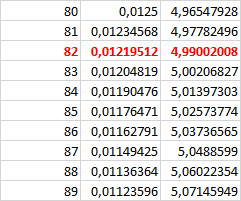
Par exemple, si l’on entre 5, le programme retourne 82.
Avec Excel
Avec un tableur, l’opération est vraiment très simple.
La première colonne est celle des premiers entiers. Deux possibilités : soit vous entrez 1 en A1 et 2 en A2 puis, après avoir sélectionner ces deux cellules vous tirez la poignée de recopie vers le bas jusqu’où vous voulez (Excel comprend ce que vous souhaitez faire), soit vous entrez 1 en A1 et la formule =A1+1 en A2, formule que vous recopiez vers le bas.
La deuxième colonne est celle des termes de la suite. En A1, vous entrez =1/A1 et vous recopiez vers le bas. Vous visualisez les \(n\) premiers inverses.
La troisième colonne est celle des sommes. Entrez =B1 en C1 puis =B2+C1 en C2. Recopiez vers le bas. Toutes les sommes partielles apparaissent mais si vous imposez un nombre déterminé de termes, seule la dernière cellule vous intéresse.
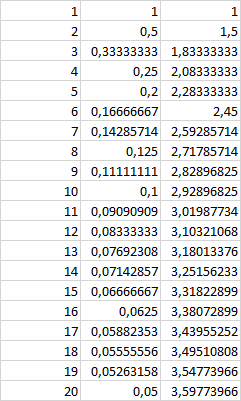
Pour vérifier le résultat obtenu avec le programme en Python ci-dessus…