Définition, patron et volume d'un cône
Chacun sait ce qu’est un cône. D’ailleurs, sa définition et le calcul de son volume sont enseignés au collège. Au lycée, il est rarement étudié mais il réapparaît dans quelques filières du supérieur.
Définition
Un cône de révolution (ou cône circulaire droit) de sommet \(S\) est le solide délimité par un disque appelé la base du cône et une portion de disque enroulée autour de la base, appelée surface latérale du cône.
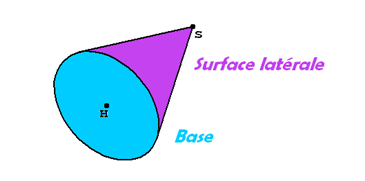
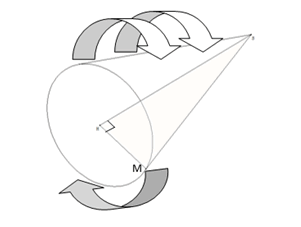
Il est engendré par la rotation d’un triangle \(SHM\) rectangle en \(H\) (\(SM\) est une génératrice). C'est d'ailleurs pour cela qu'il est appelé cône de RÉVOLUTION. Le cercle tracé par la trajectoire de \(M\) délimite la base du cône.
Patron
Le patron d’un cône est constitué d’un disque (la base) et d’une partie d’un autre disque (la surface latérale).
Connaissant la longueur de l’axe \(HS,\) la distance entre \(S\) et \(M\) est déterminée à l’aide du théorème de Pythagore.
Supposons que l’on souhaite réaliser un cône dont la base a un rayon \(HM\) de 3 cm et dont l'axe \(SH\) mesure 4 cm. Le carré de l’hypoténuse est donc égal à \(3^2 + 4^2,\) c’est-à-dire 25. La racine carrée est égale à 5. Donc, \(SM = 5.\)
Ainsi, la partie du patron qui correspond à la surface latérale est la partie d’un disque de rayon 5.
Nous savons que la circonférence de la base est égale à \(3 × 2π ≈ 18,8\) cm.
Déterminons l’angle formé au point \(S.\)
\(S\) est le centre d’un cercle dont la circonférence est égale à \(5 × 2π ≈ 31,4\) cm. Or, nous ne devons retenir que 18,8 cm.
Traduisons en degrés (problème très simple de proportionnalité) :
\(\frac{18,8 \times 360}{31,4} \approx 215°\)
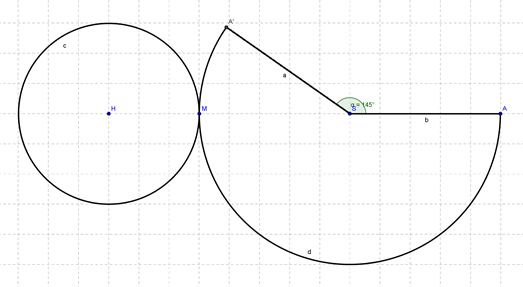
Ci-dessous, construction du patron avec Geogebra :
Volume
Soit un cône de révolution de hauteur \(h\) et dont le rayon de la base est \(r.\) Soit \(\mathscr{V}\) son volume.
\(\mathscr{V} = \frac{\pi}{3} \times r^2 \times h\)
C'est donc le tiers du cylindre de hauteur \(h\) et de rayon \(r.\)
Pour programmer cette formule avec une calculatrice TI pour le lycée, voir la page initiation à la programmation sur TI (TI-82 ou TI-83).

Tronc de cône
Si l’on tronque la partie supérieure du cône parallèlement à sa base, on obtient un tronc de cône (par exemple, un abat-jour a une forme de tronc de cône).
Si \(h\) est la hauteur du tronc de cône, si \(r\) est le rayon de la petite base et si \(R\) est le rayon de la grande base, son volume \(\mathscr{V}\) est le suivant :
\(\mathscr{V} = \frac{\pi}{3} \times h \times (R^2 + Rr + r^2)\)
Exemple : soit une bassine de 15 cm de hauteur. Le diamètre de son fond est de 25 cm et celui de son ouverture est de 40 cm. Quelle est la contenance de la bassine ?
Calcul : Le rayon du fond est de 12,5 cm et celui de l'ouverture est de 20 cm. Donc :
\(\mathscr {V}\) \(=\) \(\frac{\pi}{3} \times 15 \times [20^2 + (20 \times 12,5) + 12,5^2]\) \(=\) \(4031,25 \pi\)
Conclusion : le volume de la bassine est de 12 665 cm³ (valeur approchée), soit environ 12,7 litres.
