Exercice sur milieux et équations de droites
La géométrie ne constitue pas l'axe majeur de ce site web, plutôt orienté vers les techniques de gestion. Cependant, les programmes de maths du secondaire y ont leur place. Ainsi, prenant appui sur ceux-ci, ce site introduit quelques théorèmes et propriétés qui n'y sont pas expressément inclus mais qui les illustrent sous forme d'exercices, y compris en géométrie.
Le théorème du trapèze est de ceux-ci. Aucun rapport avec des applications économiques mais un bon support pour que des élèves de seconde s’entraînent à appliquer des propriétés de géométrie analytique dans le plan.
Dans un premier temps, énonçons le théorème. Ensuite, place à l’exercice (la version avec coordonnées de points et équations de droites et non avec les vecteurs).
Théorème
Dans un trapèze, les milieux des côtés parallèles et les intersections des diagonales sont alignés.
La démonstration peut être faite soit à partir du théorème de Thalès et des symétries, soit en utilisant les vecteurs et les propriétés de la colinéarité.
Exercice
1- Dans le plan muni d’un repère \((O\,;I ,\ J),\) placer les points \(A(-1\,; 0),\) \(B(0\,; -2),\) \(C(-5\,; -6)\) et \(D(-8\,;0).\) Tracer les six droites passant par ces points pris deux à deux.
2- Calculer les équations réduites des droites \((AB),\) \((BC),\) \((CD)\) et \((AD).\) Que peut-on en conclure à propos du quadrilatère \(ABCD\) ?
3- Calculer les coordonnées du point \(L,\) intersection des droites \((AD)\) et \((BC).\)
4- Calculer les équations réduites des droites \((AC)\) et \((BD)\) puis les coordonnées de leur point d’intersection \(M.\)
5- Calculer les coordonnées des points \(E\) et \(K,\) milieux respectifs des segments \([CD]\) et \([AB].\)
6- Calculer les coefficients directeurs des droites \((EM),\) \((EK)\) et \((EL).\)
7- Conclure.
Corrigé
1- Figure tracée à l’aide de Geogebra (pour cette question, la droite rouge ne doit pas être tracée ; l’objectif de l’exercice est justement de la définir) :
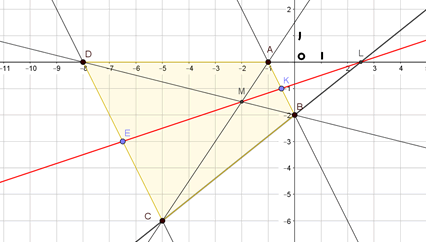
2- Équation de la droite \((AB)\)
La droite \((AB)\) n’est pas parallèle à l’axe des ordonnées car \(x_A \ne x_B.\)
On cherche alors une équation de \((AB)\) de la forme \(y = ax + b.\)
\(a\) \(=\) \(\frac{y_B - y_A}{x_B - x_A}\) \(=\) \(\frac{-2-0}{0-(-1)}\) \(=\) \(-2\)
Une équation de \((AB)\) est donc de la forme \(y = -2x + b.\) Le point \(A\) appartient à \((AB)\) donc \(0 = -2(-1) + b\) et par conséquent \(b = -2.\) La droite \((AB)\) a pour équation réduite \(y = -2x - 2.\)
De la même façon, on trouve \((BC)\) : \(y = \frac{4}{5}x - 2\) ; \((CD)\) : \(y = -2x - 16\) et \((AD)\) : \(y = 0.\)
Les droites \((AB)\) et \((CD)\) ont le même coefficient directeur contrairement à \((BC)\) et \((AD).\) Par conséquent, \(ABCD\) est un trapèze dont les bases sont \(AB\) et \(CD.\)
3- Intersection de \((AD)\) et \((BC)\)
Les coefficients directeurs de \((AD)\) et de \((BC)\)) ne sont pas égaux. \((AD)\) et \((BC)\) sont bien sécantes en un point \(L\) dont les coordonnées sont les solutions du système :
\(\left\{ {\begin{array}{*{20}{c}} {y = 0}\\ {y = \frac{4}{5}x - 2} \end{array}} \right.\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = 0}\\ {10 = 4x} \end{array}} \right.\)
\(\Leftrightarrow \left\{ {\begin{array}{*{20}{c}} {y = 0}\\ {x = 2,5} \end{array}} \right.\)
Les coordonnées de \(L\) sont \((2,5\,;0).\)
4- Équations de droites
La méthode a été détaillée en question 2. On obtient pour \((AC)\) l'équation \(y = 1,5x + 1,5\) et pour \((BD),\) \(y = -0,25x - 2.\)
Les coefficients directeurs sont différents ; \((AC)\) et \((BD)\) se croisent donc en un point \(M\) dont les coordonnées sont solutions du système :
\(\left\{ {\begin{array}{*{20}{c}} {y = 1,5x - 1,5}\\ {y = - 0,25x - 2} \end{array}} \right.\)
Nous ne détaillerons pas la résolution du système. À vous de trouver ceci :
\(\left\{ {\begin{array}{*{20}{c}} {y = -1,5}\\ {x = -2} \end{array}} \right.\)
Les coordonnées de \(M\) sont \((-2\,;-1,5).\)

5- Coordonnées de \(E,\) milieu de \([CD]\)
\(E \left(\frac{x_C+x_D}{2}\,;\frac{y_C+y_D}{2}\right)\)
\(= E \left(\frac{-5-8}{2}\,;\frac{-6+0}{2}\right)\) \(=\) \(E(-6,5\,;-3)\)
Coordonnées de \(K,\) milieu de \([AB]\)
\(K \left(\frac{-1+0}{2}\,;\frac{0-2}{2}\right)\) \(=\) \(K(-0,5\,;-1)\)
6- Coefficients directeurs
\(E\) et \(M\) n’ayant pas la même abscisse, on peut calculer le coefficient directeur de \((EM)\) :
\(a\) \(=\) \(\frac{y_M - y_E}{x_M - x_E}\) \(=\) \(\frac{-1,5+3}{-2+6,5}\) \(=\) \(\frac{1}{3}\)
Pour \((EK)\) :
\(a\) \(=\) \(\frac{-1+3}{-0,5+6,5}\) \(=\) \(\frac{1}{3}\)
Pour \((EL)\) :
\(a\) \(=\) \(\frac{-1+3}{-0,5+6,5}\) \(=\) \(\frac{1}{3}\)
7- Conclusion
Les droites \((EM),\) \((EK)\) et \((EL)\) ayant le même coefficient directeur et ayant en commun le point \(E,\) elles sont confondues. Donc, les points \(E,\) \(M,\) \(K\) et \(L\) sont alignés.
