Imputation et coûts rationnels
Parmi les charges incorporables en comptabilité de gestion, les charges fixes représentent pour le contrôleur de gestion une belle tracasserie. Comment les intégrer aux coûts des différents produits ? Tandis que certaines sont difficilement affectables, d'autres risquent de fausser les analyses par un malicieux effet pervers…
Problématique
En effet, supposons que l'on intègre chaque mois un montant forfaitaire de charges fixes au coût d'une production de nains de jardin. Si lors d'un mois donné la production diminue, leur coût unitaire augmente puisque chaque nain supporte davantage de charges fixes. Cette hausse a quelque chose d'artificiel, surtout si la baisse de production n’est que saisonnière. Et du coup, les stocks de produits finis sont surévalués. On touche ici à l’une des limites de la méthode des centres d'analyse…
La technique de l’imputation rationnelle (IR) apporte heureusement une réponse.
L'imputation rationnelle
L’idée est de partir d’un niveau d’activité normal qui va servir de référence. On définit ainsi un coefficient d’imputation rationnelle :
\(\displaystyle{C_{IR} = \frac{\scr{activité\;réelle}}{\scr{activité\;normale}}}\)
Appliqué aux charges fixes, ce coefficient permet d'en moduler la pondération dans les coûts globaux. On obtient alors des charges fixes imputées qui ne polluent pas les variations de coûts unitaires par un calcul trop rigide. Ajoutées aux charges variables, elles permettent d’obtenir un coût de revient appelé « coût rationnel ».
En période de sous-activité, une partie de ces charges n’est pas imputée aux coûts rationnels. C’est un coût de chômage. En revanche, lorsque l’activité est supérieure à la normale, les coûts rationnels intègrent un bonus de suractivité.
Précisions techniques : pour établir le coût rationnel d’une unité d’œuvre, il faut procéder à l’IR AVANT la répartition des charges fixes dans les centres d’analyse (prestations réciproques et répartition secondaire). Autre mise en garde : l’activité normale est considérée hors temps habituel de non-production (réglage des machines, pauses…), et hors contraintes exogènes non liées à l’activité (grèves, pannes, goulots d’étranglement, météo…).
Le graphique ci-dessous illustre le niveau d’un coût complet en fonction de l’activité (quantités produites, heures machines…) et celui d’un coût rationnel. La représentation de ce dernier est particulièrement facile à tracer puisque la droite part de l’origine et croise la courbe de coût au niveau d’activité normale. Les différences d’imputation sont les zones marquées de doubles flèches noires.
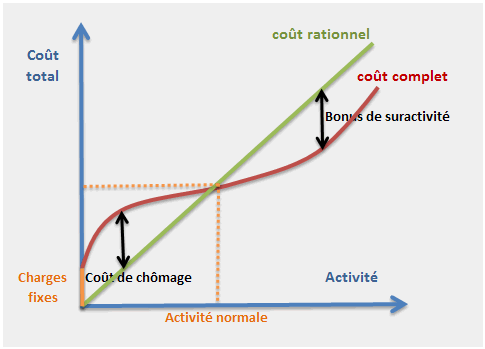
Note : dans la mesure où l’étude porte sur du court terme, l’activité présente rarement une vaste plage de possibilités et la courbe est alors approximée par une droite.
Avantages et inconvénients
Cette technique est tout indiquée pour les activités saisonnières mais aussi comme outil de valorisation des stocks de produits finis et de détermination d’un prix de vente.
Elle permet aussi d'établir des devis plus justes. En période de suractivité, les prix établis sur la base des coûts ne sont pas minorés. Au contraire, en cas de sous-activité, les clients ne paient pas davantage pour compenser une conjoncture défavorable.
Pourtant, elle n’est pas très courante…
Certes, il est parfois difficile de distinguer les charges fixes des variables, entre autres problèmes (voir les limites des coûts complets). Mais une difficulté propre à la méthode réside dans la définition de l’activité normale.
Enfin, une possible différence d’appréciation du niveau normal d’activité entre plusieurs centres d’analyse peut conduire à des montages très compliqués.
Exemple
Des martiens fabriquent quelques reproductions miniatures des grandes soucoupes volantes qui ont marqué leur histoire. S’intéressant de près à la production du modèle Z0, ils souhaitent mettre en place l’imputation rationnelle. Les charges fixes mensuelles affectées à cette production s’établissent à 1 200 unités monétaires et 600 soucoupes ont été réalisées ce mois-ci (activité normale : 750 soucoupes). 500 soucoupes seulement ont été vendues, les autres étant stockées (il n’existait aucun stock au début du mois).

Comparons le coût complet et le coût rationnel de production puis déterminons le coût de sous-activité.
Sans IR, le coût de production est le suivant :
| Charges fixes | 1 200 |
| Charges variables | 24 000 |
| Coût de production | 25 200 |
| Quantité produite | 600 |
| Coût unitaire | 42 |
Le coefficient d’IR est de \(\frac{600}{750} = 0,8.\)
Donc, charges fixes imputées : \(0,8 × 1\,200 = 960.\)
Coût unitaire de production avec IR :
| Charges fixes | 960 |
| Charges variables | 24 000 |
| Coût de production | 24 960 |
| Quantité produite | 600 |
| Coût unitaire | 41,60 |
Le « véritable » coût de production d’une Z0 est donc sans doute plus proche de 41,60 que de 42.
Le stock de produits s’établit ainsi à 100 soucoupes évaluées à 41,60, soit 4 160 unités monétaires. Sans l’IR, il aurait été estimé à 4 200.
Le coût de sous-activité s’élève à 240. Une partie de ce coût est à affecter aux stocks et l’autre partie à la production vendue.
Stocks : \(240 × \frac{100}{600} = 40.\) On retrouve la différence entre 4 200 et 4 160.
Ventes : \(240 × \frac{500}{600} = 200.\)
Un exemple plus développé figure en page d'exercice sur imputation rationnelle.
